Spell Check in Jupyter Notebook
The purpose of this post is to show how to have automatic spell check in Jupyter Notebook, as shown below.
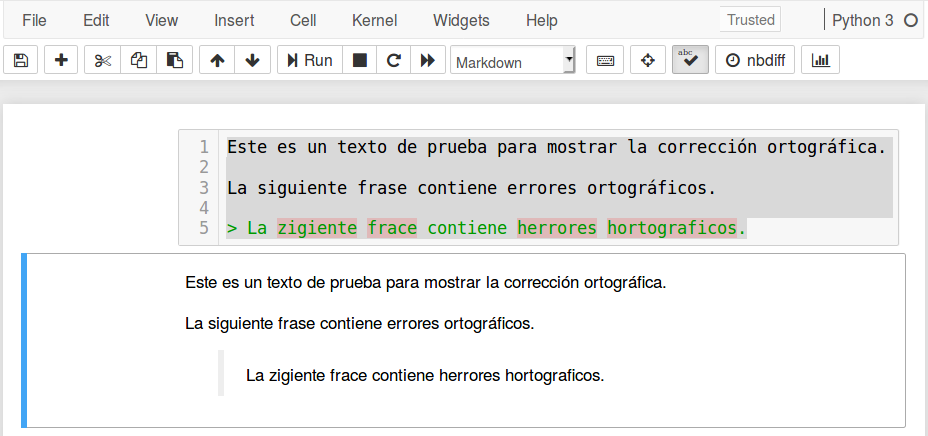
There are several ways to do this. However, the easiest way is through the (nbextension) Spellchecker. plugin.
Step by step
The steps to follow are those:
Install Jupyter notebook extensions (nbextensions). This includes Spellchecker.
Locate the dictionaries in the folder where the plugin is. Dictionaries must use UTF-8 encoding.
Configure the path of the dictionaries. This can be a URL or a path relative to the folder where the plugin is located.
We will describe each step in detail below.
Step 1: Install nbextensions
There is a list of plugins that add some commonly used functionality to the Jupyter notebook.
Type the following in a terminal, to install it using PIP.
However, if Anaconda is being used the recommended method is to use
conda, as shown below.
This should install the plugins and also the configuration interface. In the main menu of Jupyter notebook a new tab named Nbextension will appear. Here you can choose the add-ons to use. The appearance is as follows.
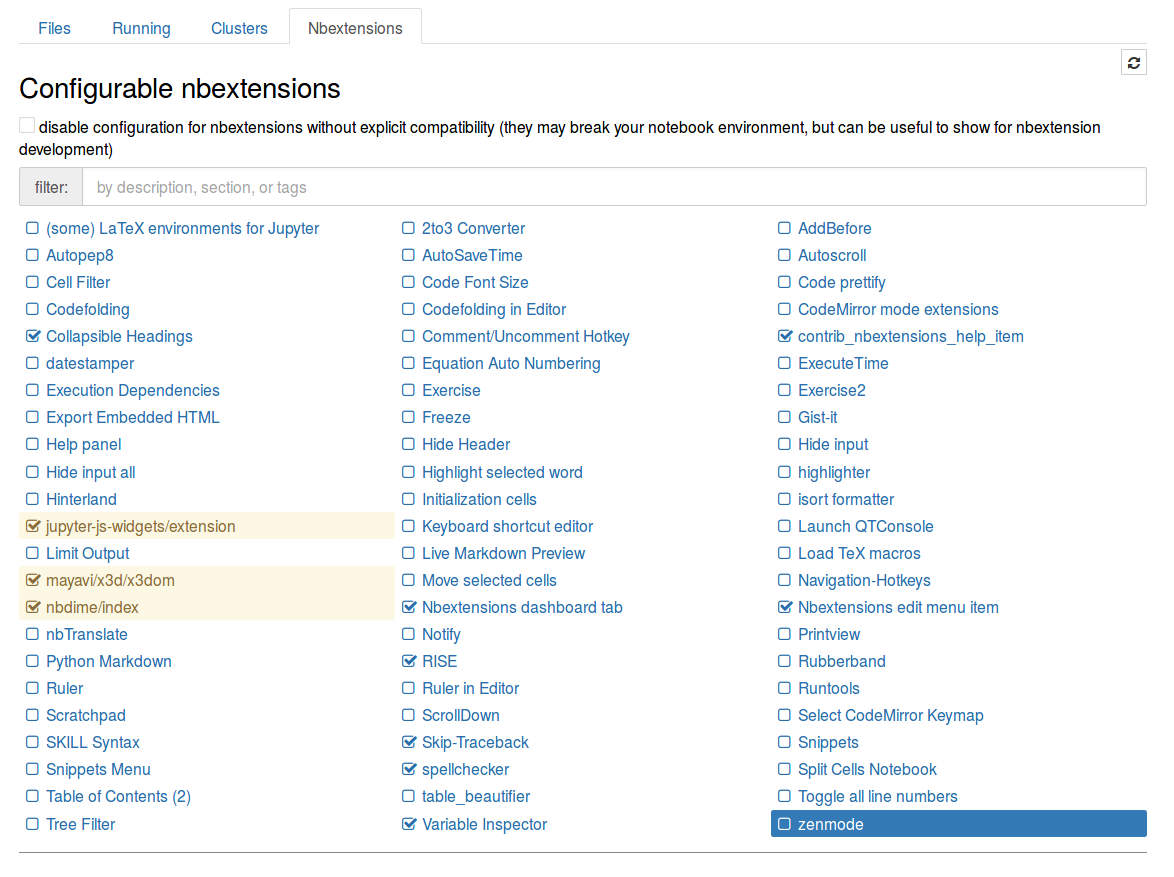
Some recommended plugins are:
Collapsible Headings: that allows to hide sections of the documents.
RISE: that turns notebooks into presentations.
Step 2: Dictionaries for Spanish
The documentation of Spellchecker suggests using a Python script to download dictionaries from project Chromium. However, these are encoded in ISO-8859-1 (western) and it fails for characters with accents or tildes. So, to avoid problems the dictionary must be UTF-8. They can be downloaded at this link.
Once you have the dictionaries, they must be located in the path of the plugin. On my computer this would be
and within this we will place them in
This location is arbitrary, the important thing is that we need to know the relative path to the plugin.
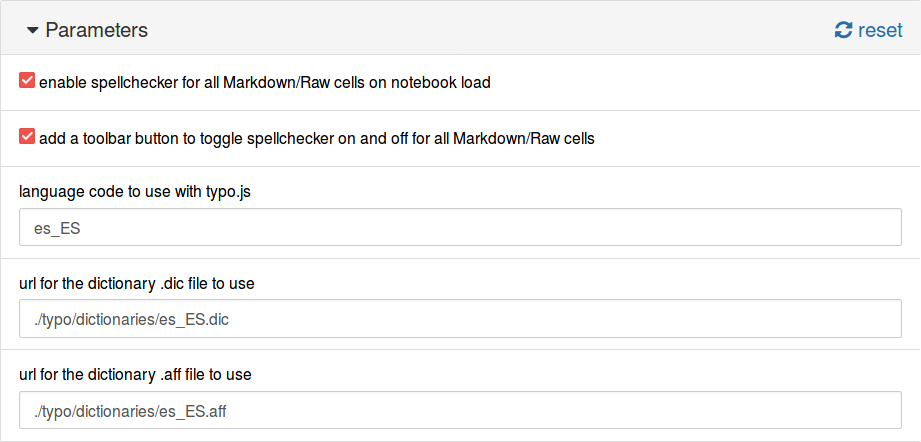
Step 3: Plugin Configuration
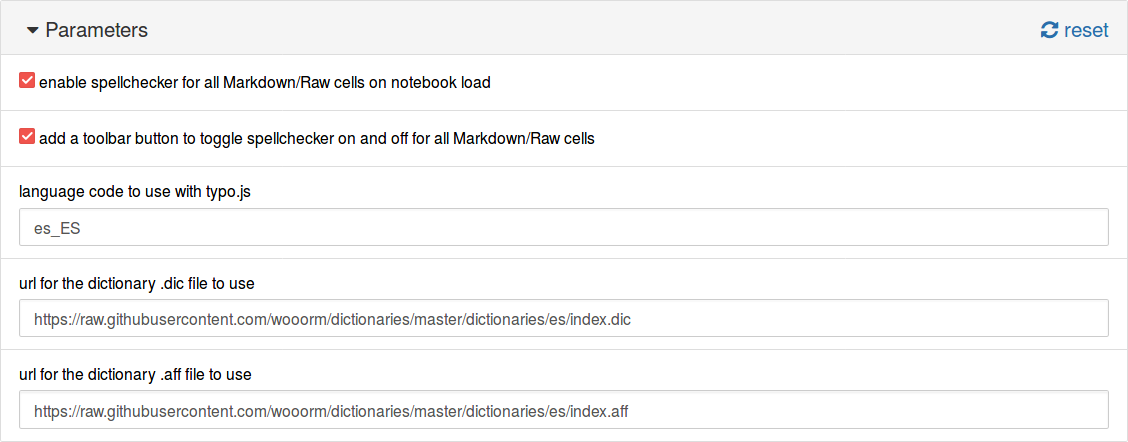
Now, in the Nbextensions tab we select the plugin and fill the fields with the information from our dictionary:
language code to use with typo.js:
es_ESurl for the dictionary .dic file to use:
./typo/dictionaries/es_ES.dicurl for the dictionary .aff file to use:
./typo/dictionaries/es_ES.aff
This is shown below.
Another option is to use the URL for the files. The dictionaries of the project hunspell in UTF-8 are available at https://github.com/wooorm/dictionaries. In this case, the configuration would be:
language code to use with typo.js:
es_ESurl for the dictionary .dic file to use:
https://raw.githubusercontent.com/wooorm/dictionaries/master/dictionaries/es/index.dicurl for the dictionary .aff file to use:
https://raw.githubusercontent.com/wooorm/dictionaries/master/dictionaries/es/index.aff
And it is shown below.