Skip to main content

Nicolás' blog

Isometric graphics in Inkscape: Part 2

Nicolás Guarín-Zapata

Comments

Also available in:

Español

Last week I posted a quick guide on isometric drawing using Inkscape. In that post, I showed how to obtain images that are projected to the faces of an isometric box.

After my post, I was asked by Biswajit Banerjee on Twitter if I could repeat the process with a more complex example, and he suggested the following schematic

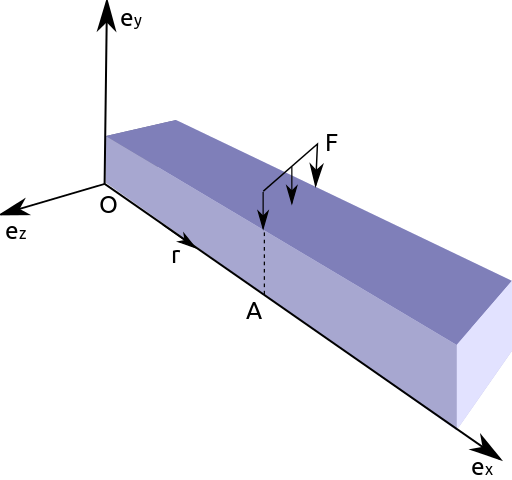
Computing the moment of force in a beam

which, I guess, was created in Inkscape using the "Create 3D Box" option.

In this post, I will:

  1. Use the same approach from last week to recreate this schematic

  2. Suggest my preferred approach for drawing this schematic

First approach

I will repeat the cheatsheet from last week. Keep in mind that Inkscape treats clockwise rotation as positive. Opposite to common notation in mathematics.

Cheatsheet for isometric schematics in Inkscape

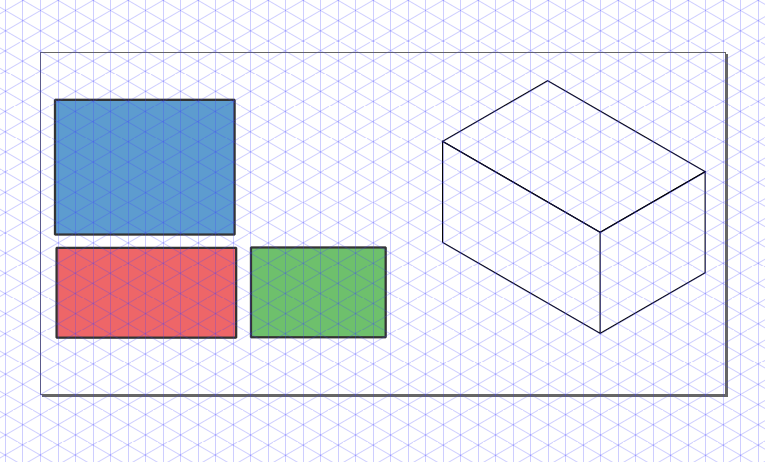
Then, to create a box with desired dimensions we first create each rectangle with the right dimensiones (in parallel projections). In the following example we used faces with aspect ratios 3:2, 2:1 and 4:3. The box at the right is the figure obtained after applying the transformations described in the previous schematic.

Orthogonal views and final isometric figure

We can now proceed, to recreate the desired figure. I don't know the exact dimensions of the box; my guess is that the cross-section was a square and the aspect ratio was 5:1. After applying the transformations to each rectangle we obtain the following (adding some tweaks here and there).

Recreated figure using the described approach

Second approach

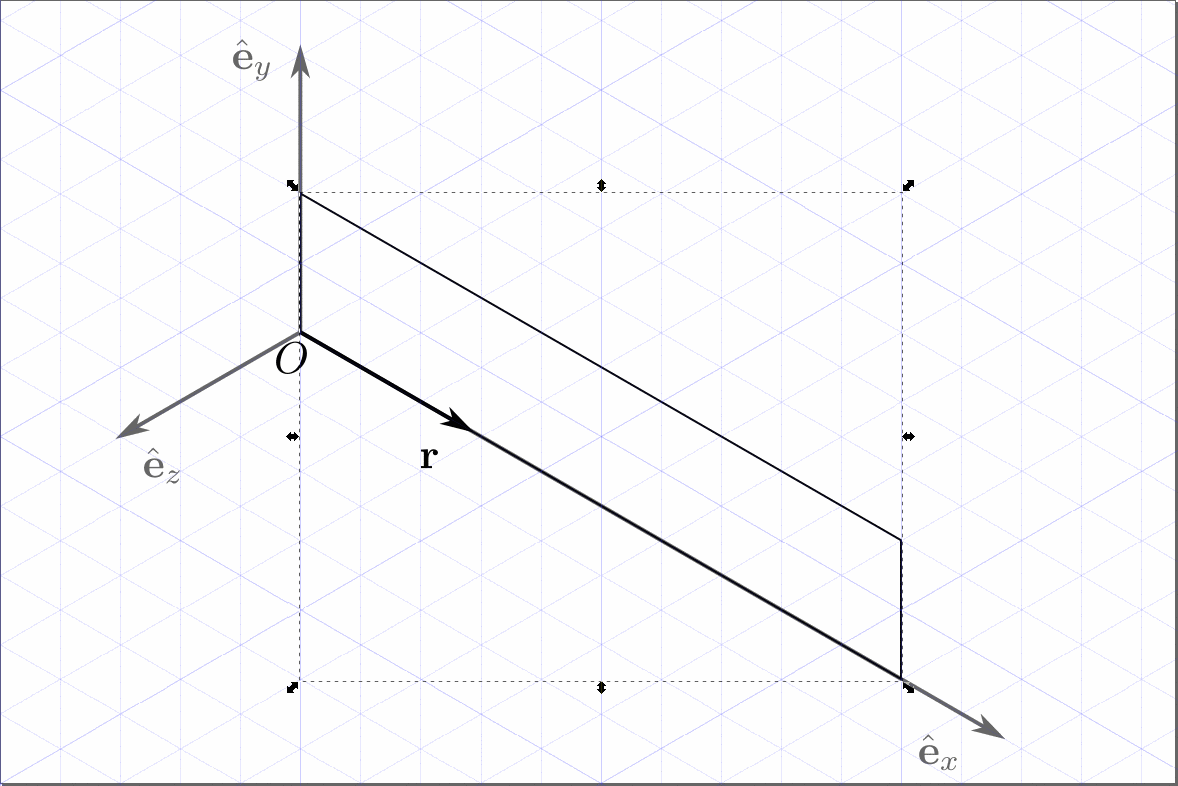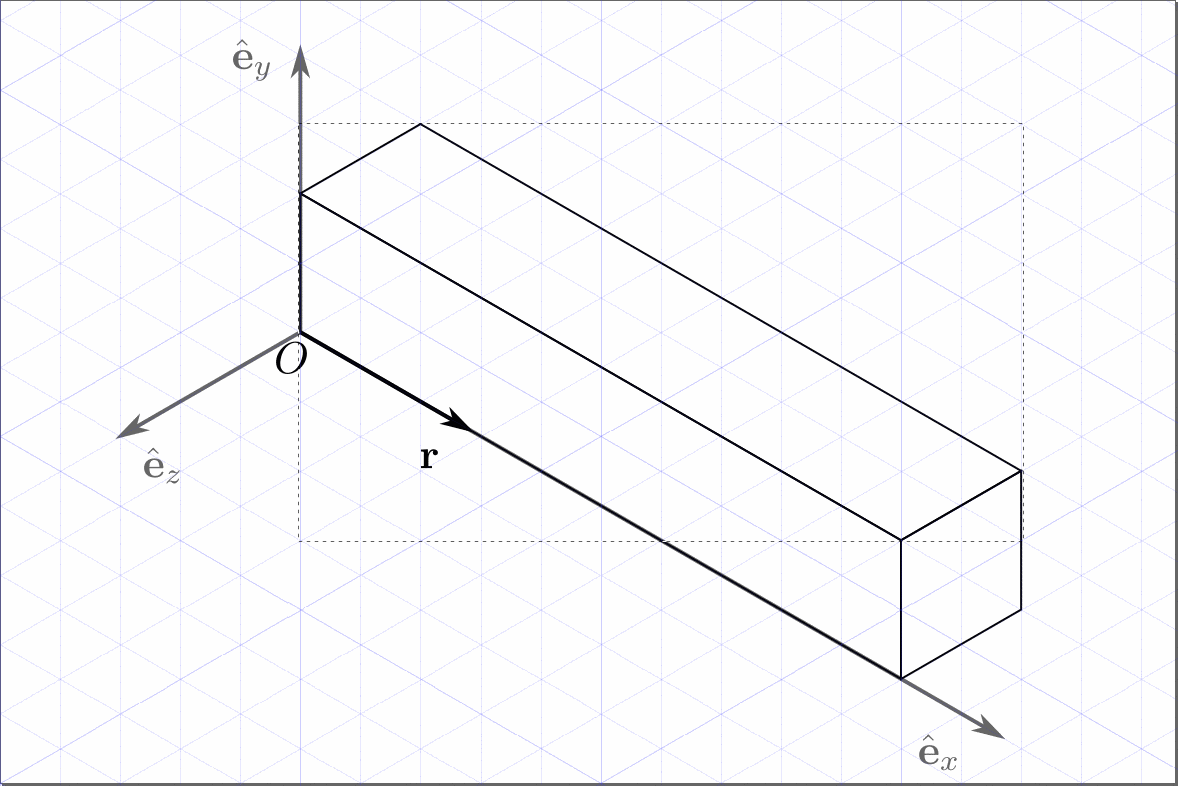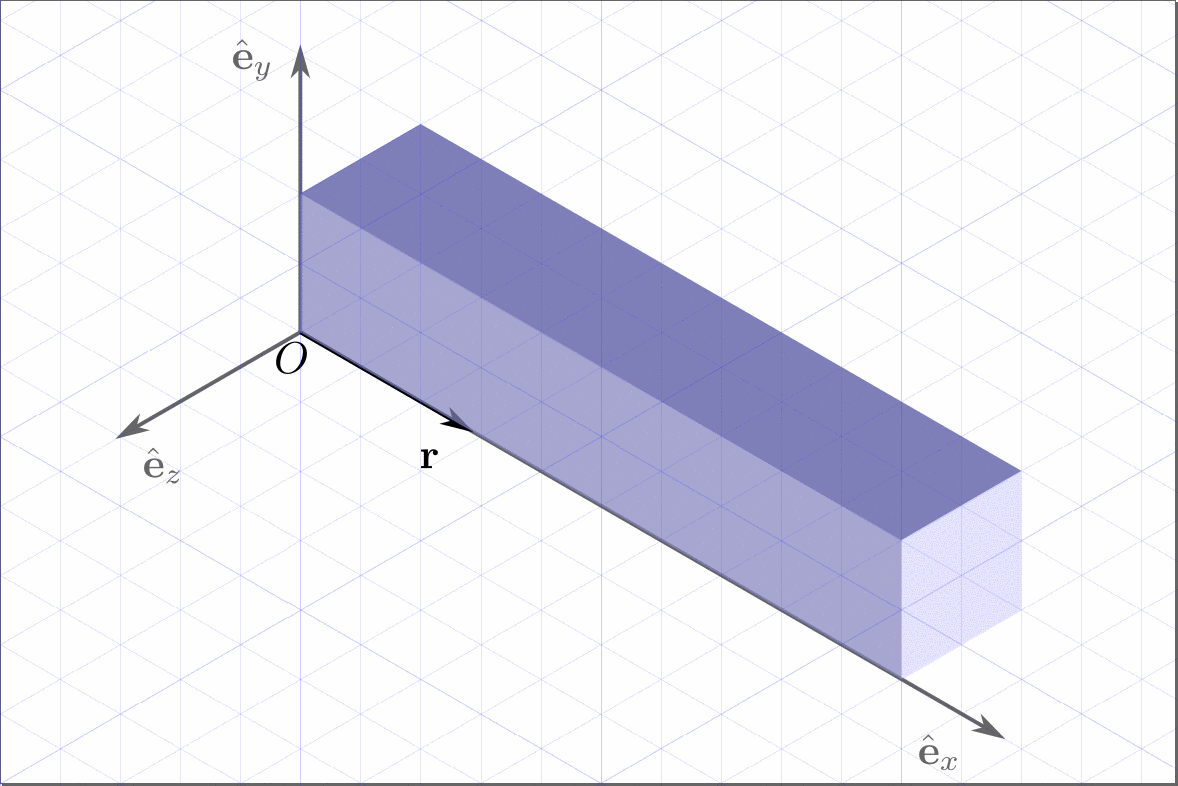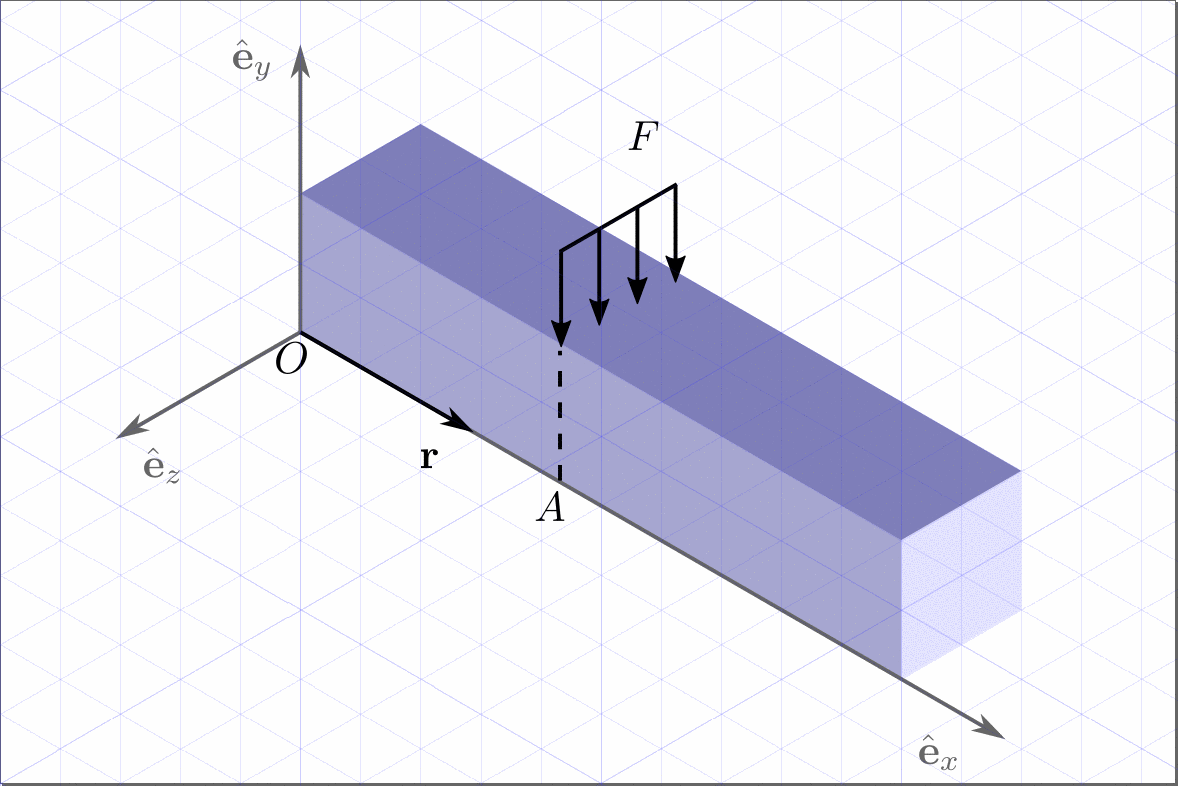
For this type of schematic, I would prefer to create an axonometric grid (File > Document Properties > Grids). After adding the grid to our canvas it is pretty straightforward to draw the figures in isometric view. The canvas should look similar to the following image.

Second approach: using an axonometric grid

We can then draw each face using the grid. If we want to be more precise we can activate Snap to Cusp Nodes. The following animation shows the step by step construction.

Step by step construction of the isometric

And we obtain the final image.

Recreated figure using the second approach

Conclusion

As I mentioned, Inkscape can be used for drawing simple figures in isometric projection. Nevertheless, I strongly suggest to use a CAD like FreeCAD for more complicated geometries.

Comments

Comments powered by Disqus