Comparación de mapas de colores cíclicos

Nicolás Guarín-Zapata

2018-01-02 18:55

También disponible en:

Empecé esta publicación buscando implementaciones de mapas de difusión en Python, que no pude encontrar. Me puse entonces a seguir un ejemplo sobre aprendizaje de variedades de Jake Vanderplas en un conjunto de datos diferente. Y funcionó bien

/images/manifold_learning_toroidal_helix.svg

pero el mapa de color es "Spectral", que es divergente. Esto me puso a pensar acerca de usar un mapa de colores cícliclo, y terminé en esta pregunta de StackOverflow. Y decidí comparar algunos mapas de colores cíclicos.

Elegí mapas de colores de diferentes fuentes

cmocean:
- phase
Paraview:
- hue_L60
- erdc_iceFire
- nic_Edge
Colorcet:
- colorwheel
- cyclic_mrybm_35_75_c68
- cyclic_mygbm_30_95_c78

y, obviamente, hsv. Los mapas de colores en formato de texto plano se pueden descargar aquí.

Comparación

Para todos los ejemplos se importaron los siguientes módulos:

from __future__ import division, print_function
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from colorspacious import cspace_convert

Imagen de prueba

Peter Kovesi propuso una manera de comparar mapas de colores cíclicos en un artículo en 2015. Consta de una rampa en espiral con ondulaciones. En coordenadas polares es

\begin{equation*} c = (A \rho^p \sin(n \theta) + \theta)\, \mathrm{mod}\, 2\pi \end{equation*}

con \(A\) la amplitud de la oscilación, \(\rho\) el radio normalizado en [0, 1], \(p\) un número positivo, y \(n\) el número de ciclos.

Y la siguiente función crea la rejilla en Python.

def circle_sine_ramp(r_max=1, r_min=0.3, amp=np.pi/5, cycles=50,
                     power=2, nr=50, ntheta=1025):
r, t = np.mgrid[r_min:r_max:nr*1j, 0:2*np.pi:ntheta*1j]
r_norm = (r - r_min)/(r_max - r_min)
vals = amp * r_norm**power * np.sin(cycles*t) + t
vals = np.mod(vals, 2*np.pi)
return t, r, vals

El resultado es el siguiente

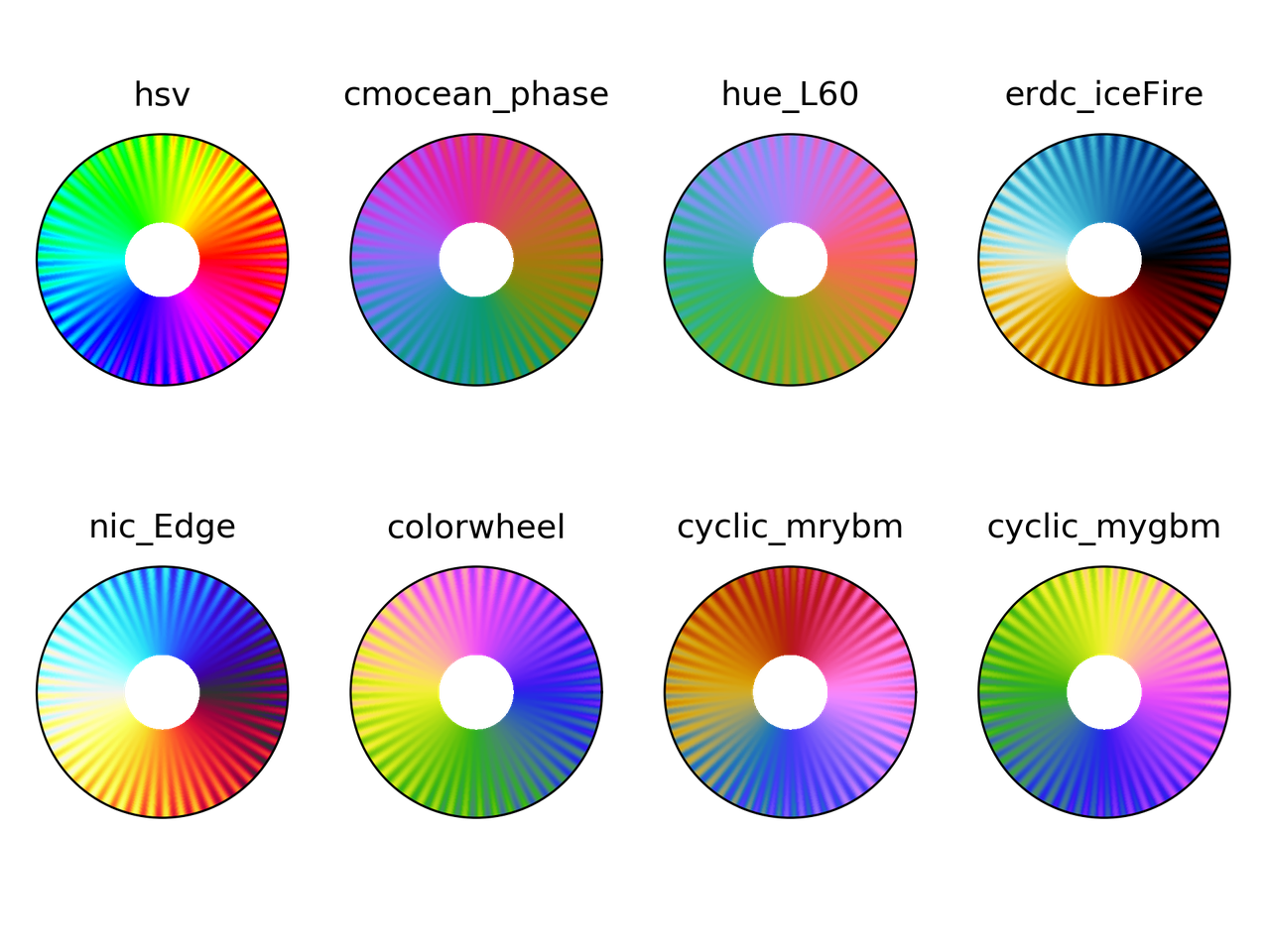
Prueba para daltonismo

t, r, vals = circle_sine_ramp(cycles=0)
cmaps = ["hsv",
         "cmocean_phase",
         "hue_L60",
         "erdc_iceFire",
         "nic_Edge",
         "colorwheel",
         "cyclic_mrybm",
         "cyclic_mygbm"]
severity = [0, 50, 50, 50]
for colormap in cmaps:
    data = np.loadtxt(colormap + ".txt")
    fig = plt.figure()
    for cont in range(4):
        cvd_space = {"name": "sRGB1+CVD",
             "cvd_type": cvd_type[cont],
             "severity": severity[cont]}
        data2 = cspace_convert(data, cvd_space, "sRGB1")
        data2 = np.clip(data2, 0, 1)
        cmap = LinearSegmentedColormap.from_list('my_colormap', data2)
        ax = plt.subplot(2, 2, 1 + cont, projection="polar")
        ax.pcolormesh(t, r, vals, cmap=cmap)
        ax.set_xticks([])
        ax.set_yticks([])
    plt.suptitle(colormap)
    plt.tight_layout()
    plt.savefig(colormap + ".png", dpi=300)

/images/hsv_eval.png — Comparación de `hsv` para diferentes deficiencias visuales del color.

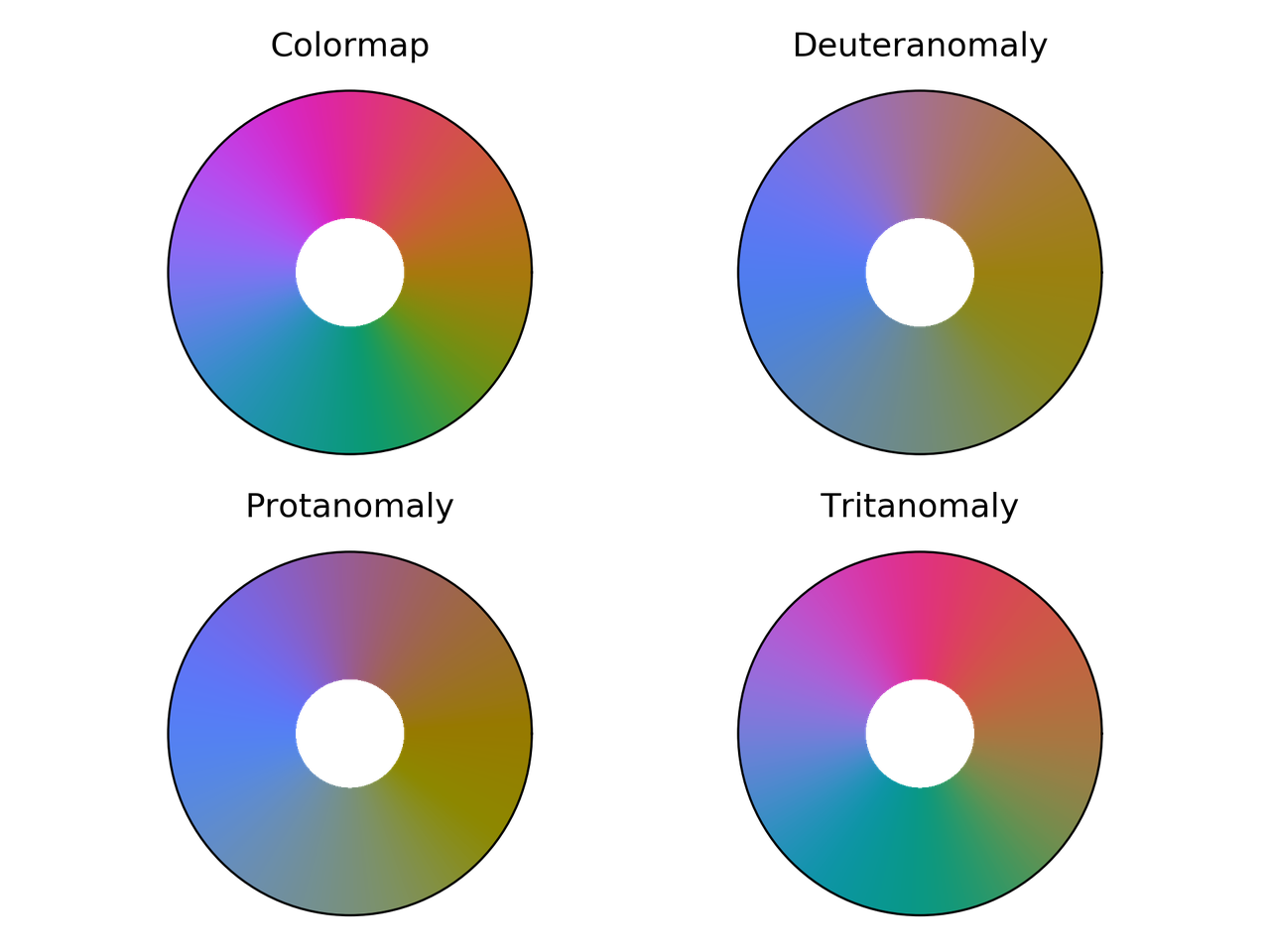
/images/cmocean_phase_eval.png — Comparación de `Phase` para diferentes deficiencias visuales del color.

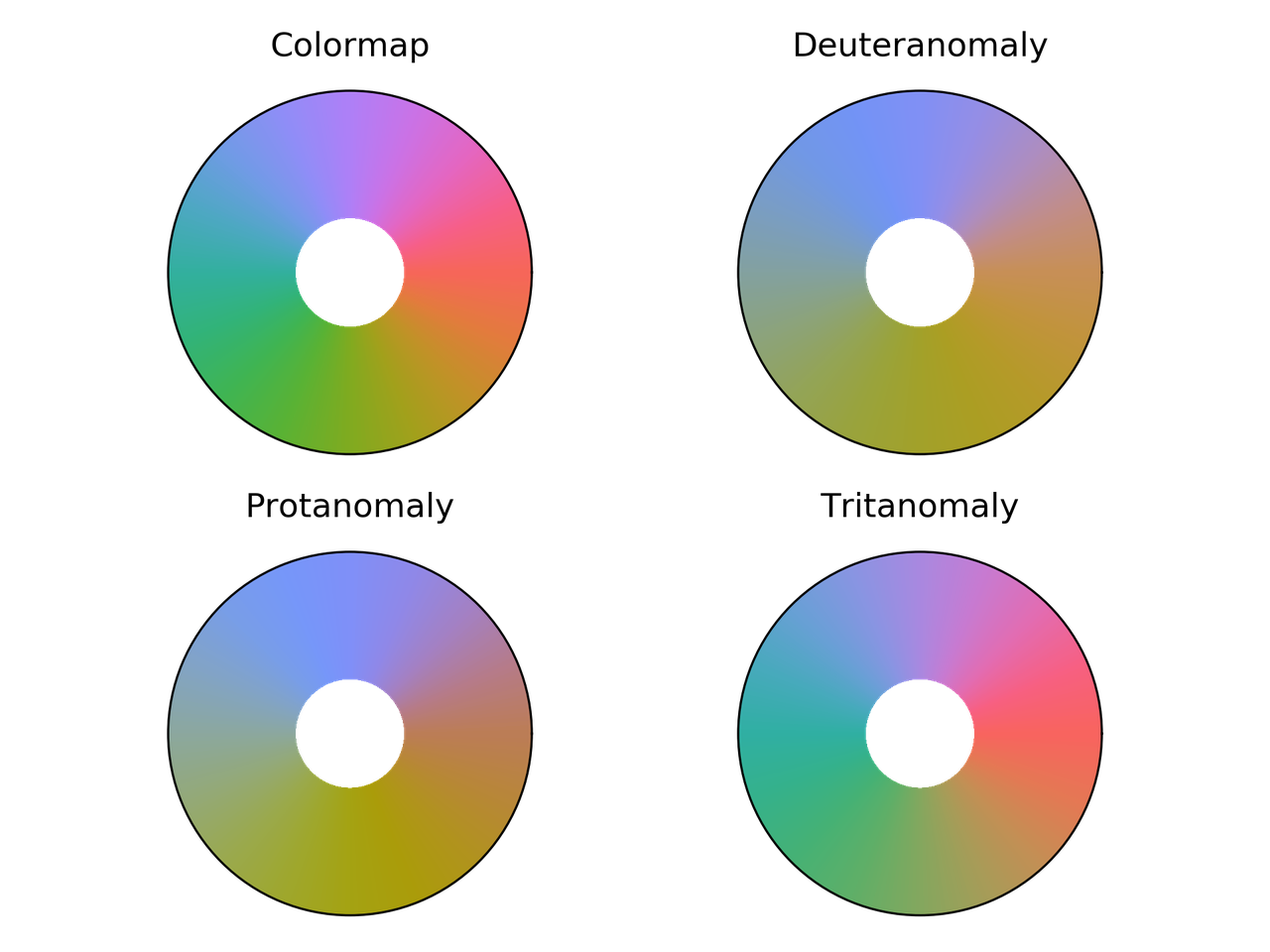
/images/hue_L60_eval.png — Comparación de `hue_L60` para diferentes deficiencias visuales del color.

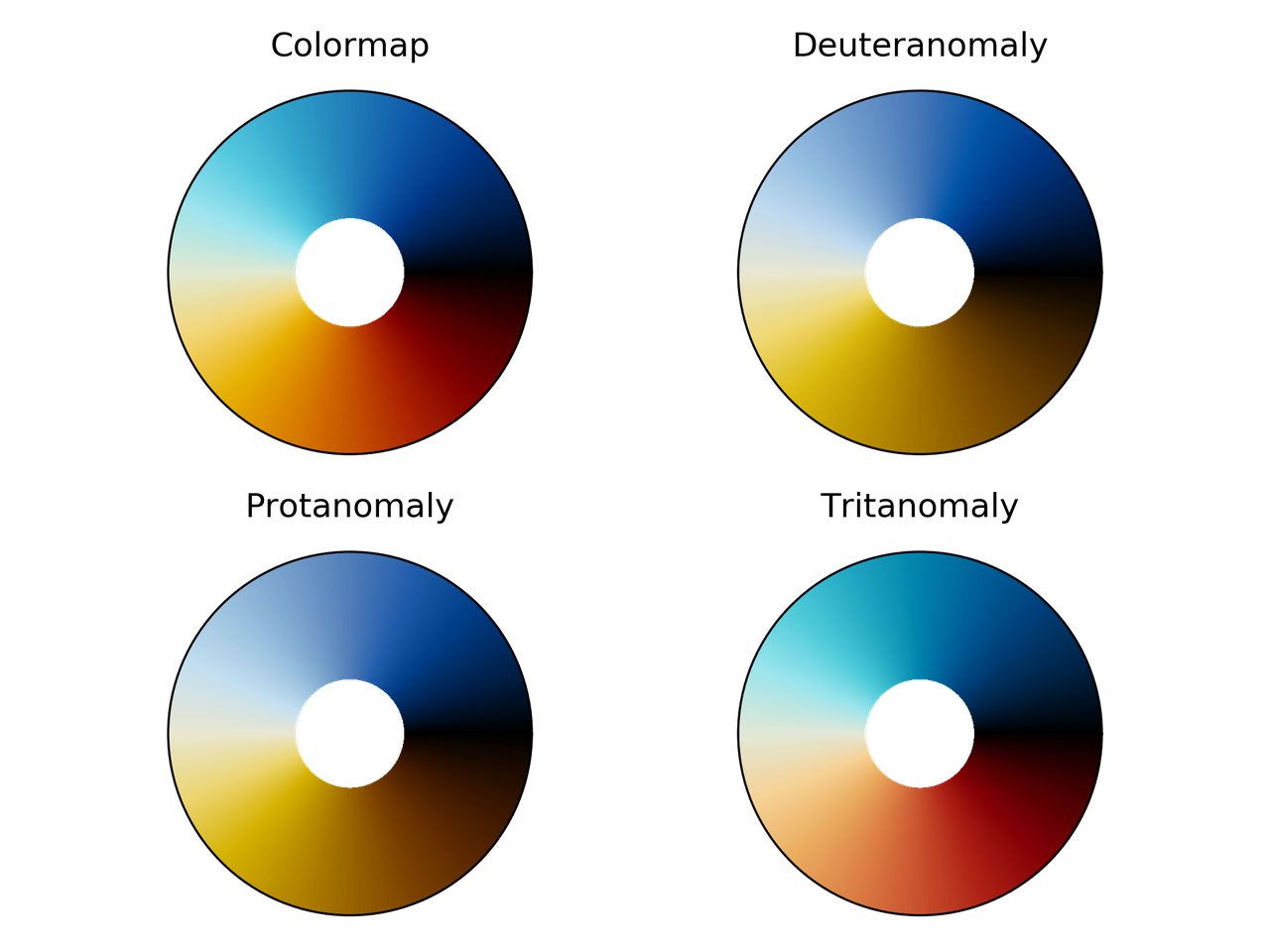
/images/erdc_iceFire_eval.png — Comparación de `erdc_iceFire` para diferentes deficiencias visuales del color.

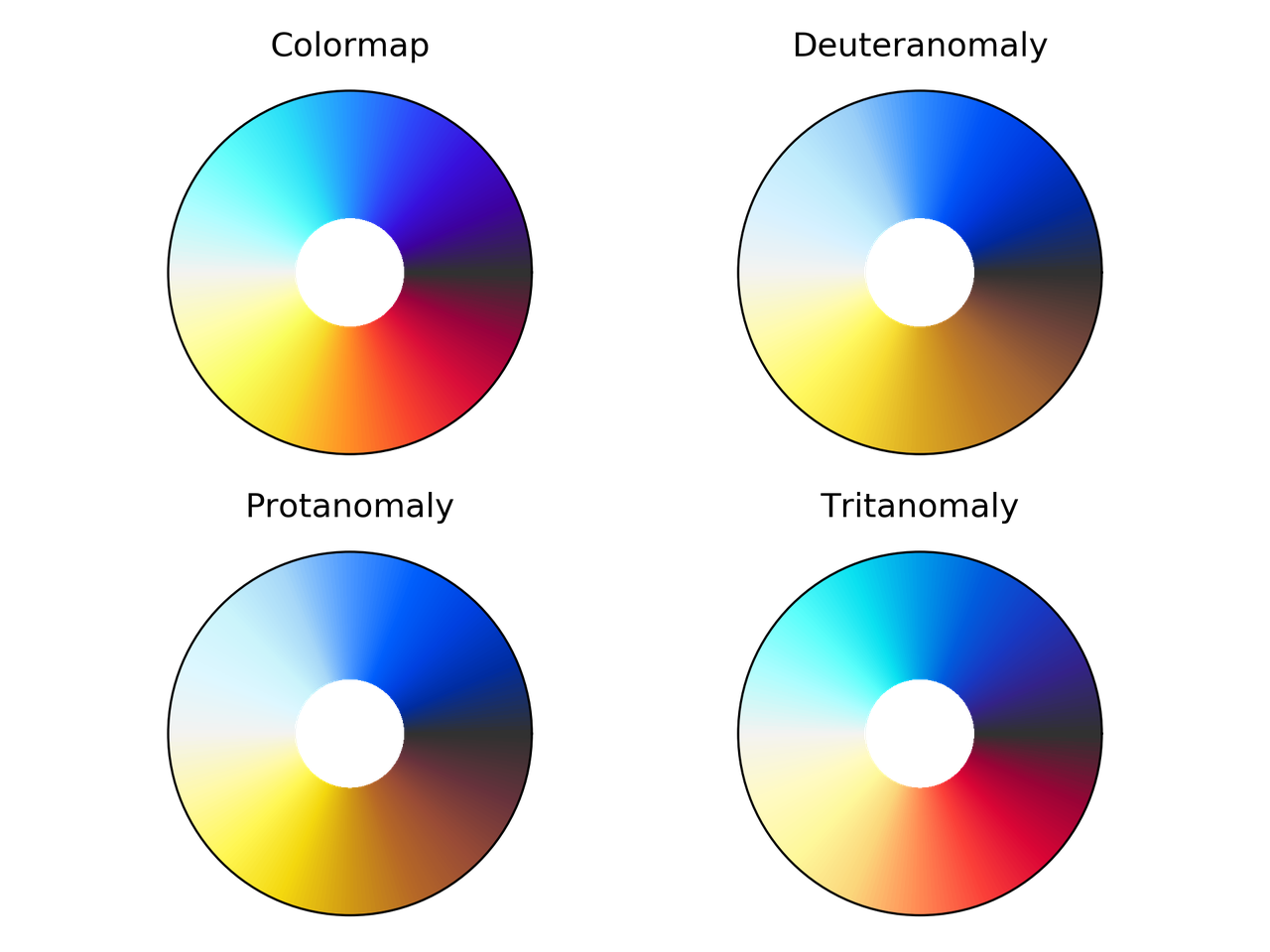
/images/nic_Edge_eval.png — Comparación de `nic_Edge` para diferentes deficiencias visuales del color.

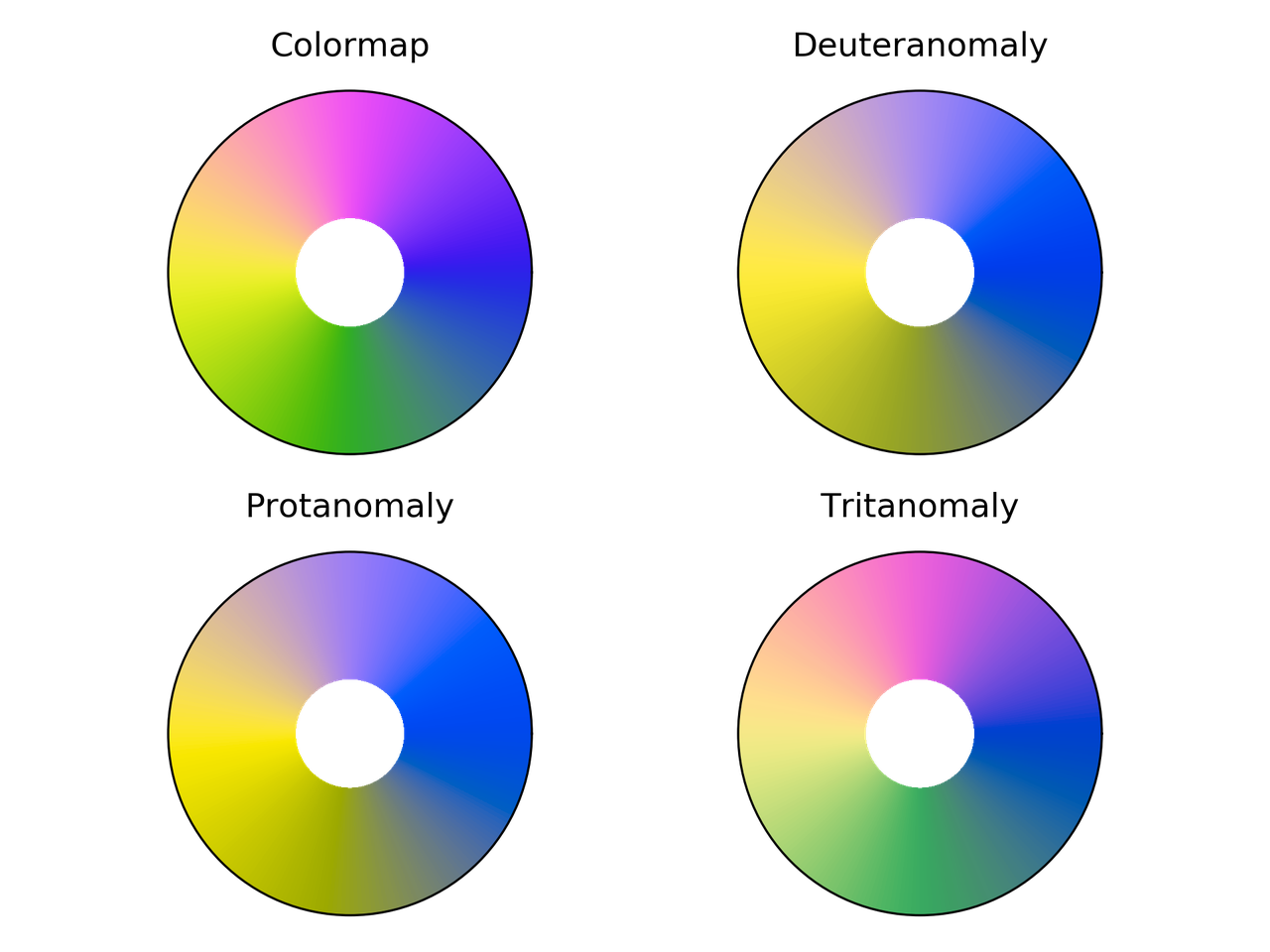
/images/colorwheel_eval.png — Comparación de `Colorwheel` para diferentes deficiencias visuales del color.

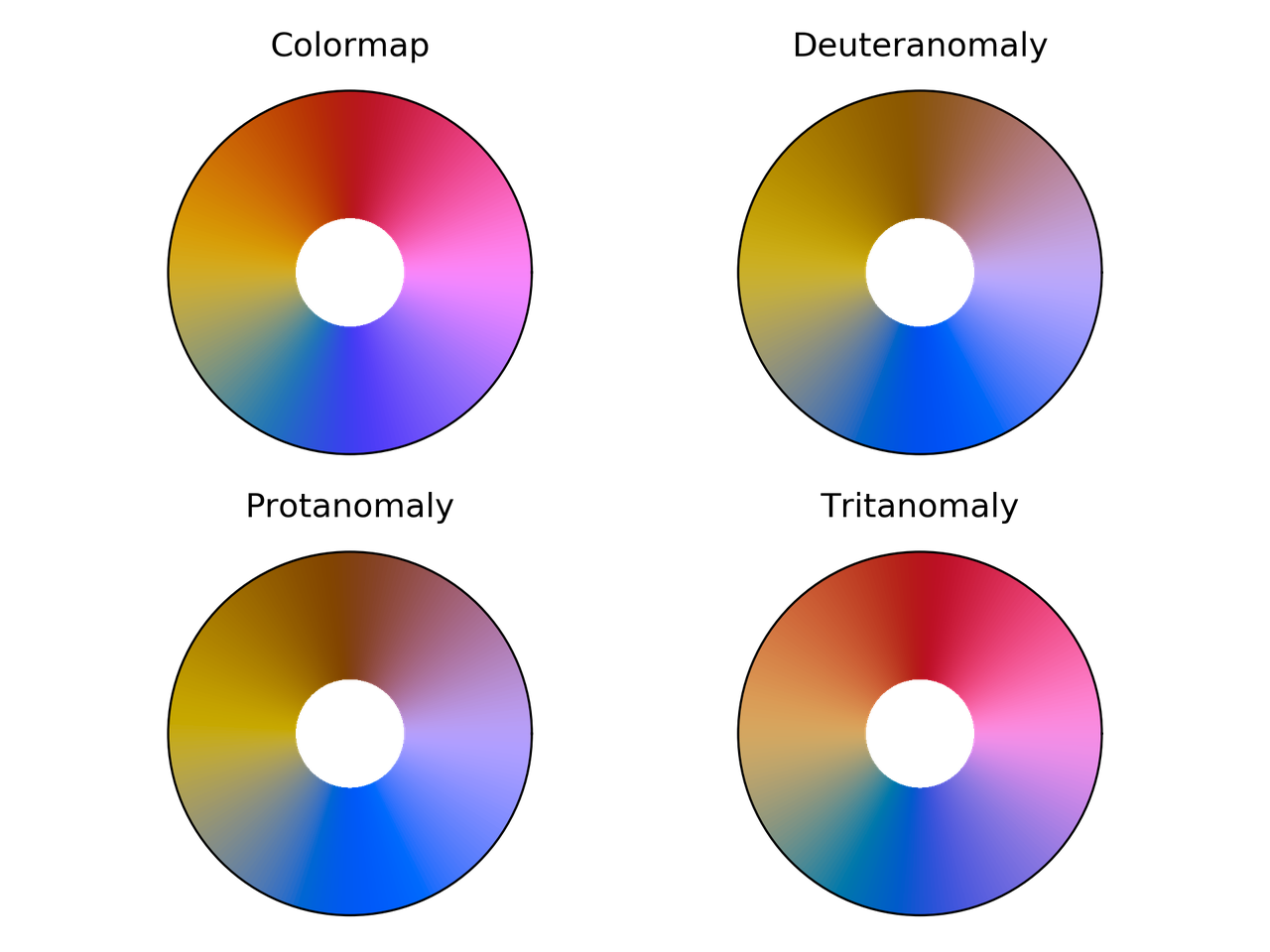
/images/cyclic_mrybm_eval.png — Comparación de `Cyclic_mrybm` para diferentes deficiencias visuales del color.

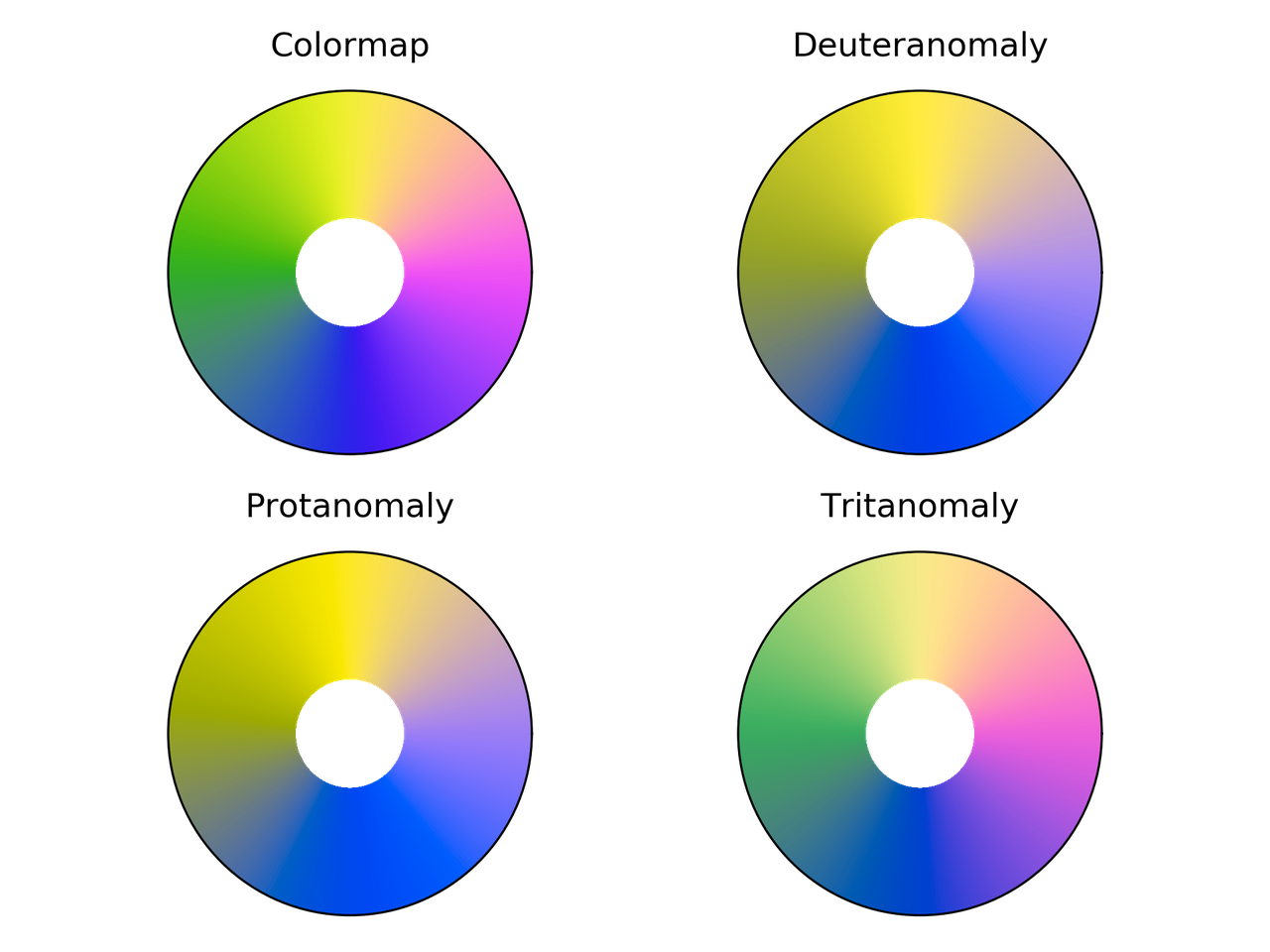
/images/cyclic_mygbm_eval.png — Comparación de `Cyclic_mygbm` para diferentes deficiencias visuales del color.

Mapas de colores cíclicos generados aleatoriamente

¿Qué pasa si generamos mapas de colores cíclicos aleatoriamente? ¿Cómo lucirían?

A continuación están las piezas de código y mapas de colores resultantes.

from __future__ import division, print_function
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap


# Next line to silence pyflakes. This import is needed.
Axes3D

plt.close("all")
fig = plt.figure()
fig2 = plt.figure()
nx = 4
ny = 4
azimuths = np.arange(0, 361, 1)
zeniths = np.arange(30, 70, 1)
values = azimuths * np.ones((30, 361))
for cont in range(nx * ny):
    np.random.seed(seed=cont)
    rad = np.random.uniform(0.1, 0.5)
    center = np.random.uniform(rad, 1 - rad, size=(3, 1))
    mat = np.random.rand(3, 3)
    rot_mat, _ = np.linalg.qr(mat)
    t = np.linspace(0, 2*np.pi, 256)
    x = rad*np.cos(t)
    y = rad*np.sin(t)
    z = 0.0*np.cos(t)
    X = np.vstack((x, y, z))
    X = rot_mat.dot(X) + center

    ax = fig.add_subplot(ny, nx, 1 + cont, projection='polar')
    cmap = LinearSegmentedColormap.from_list('my_colormap', X.T)
    ax.pcolormesh(azimuths*np.pi/180.0, zeniths, values, cmap=cmap)
    ax.set_xticks([])
    ax.set_yticks([])

    ax2 = fig2.add_subplot(ny, nx, 1 + cont, projection='3d')
    ax2.plot(X[0, :], X[1, :], X[2, :])
    ax2.set_xlim(0, 1)
    ax2.set_ylim(0, 1)
    ax2.set_zlim(0, 1)
    ax2.view_init(30, -60)
    ax2.set_xticks([0, 0.5, 1.0])
    ax2.set_yticks([0, 0.5, 1.0])
    ax2.set_zticks([0, 0.5, 1.0])
    ax2.set_xticklabels([])
    ax2.set_yticklabels([])
    ax2.set_zticklabels([])


fig.savefig("random_cmaps.png", dpi=300, transparent=True)
fig2.savefig("random_cmaps_traj.svg", transparent=True)

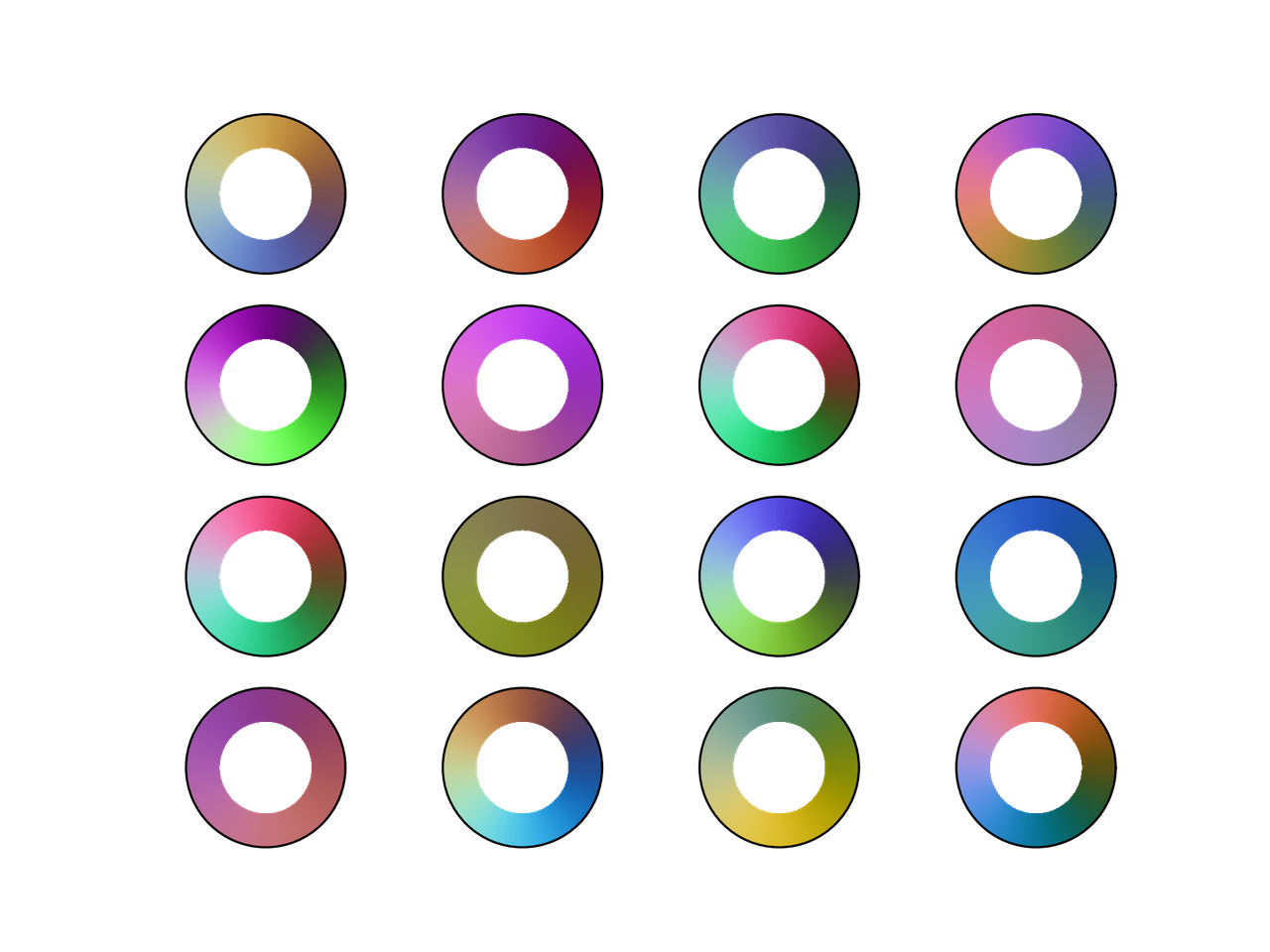
/images/random_cmaps.png — 16 mapas de colores generados aleatoriamente.

/images/random_cmaps_traj.svg — Trayectorias en espacio RGB para los mapas de colores generados aleatoriamente.

Una idea interesante sería tomar estos mapas de colores y optimizar algunos parámetros perceptuales como luminosidad para obtener mapas de colores útiles.

Conclusiones

Probablemente, yo usaría phase, colorwheel, o mrybm en el futuro.

/images/toroidal_helix_phase.svg — Imagen inicial usando `phase`.

/images/toroidal_helix_colorwheel.svg — Imagen inicial usando `colorwheel`.

/images/toroidal_helix_mrybm.svg — Imagen inicial usando `mrybm`.

Referencias

Peter Kovesi. Good Colour Maps: How to Design Them. arXiv:1509.03700 [cs.GR] 2015

Nicolás' blog