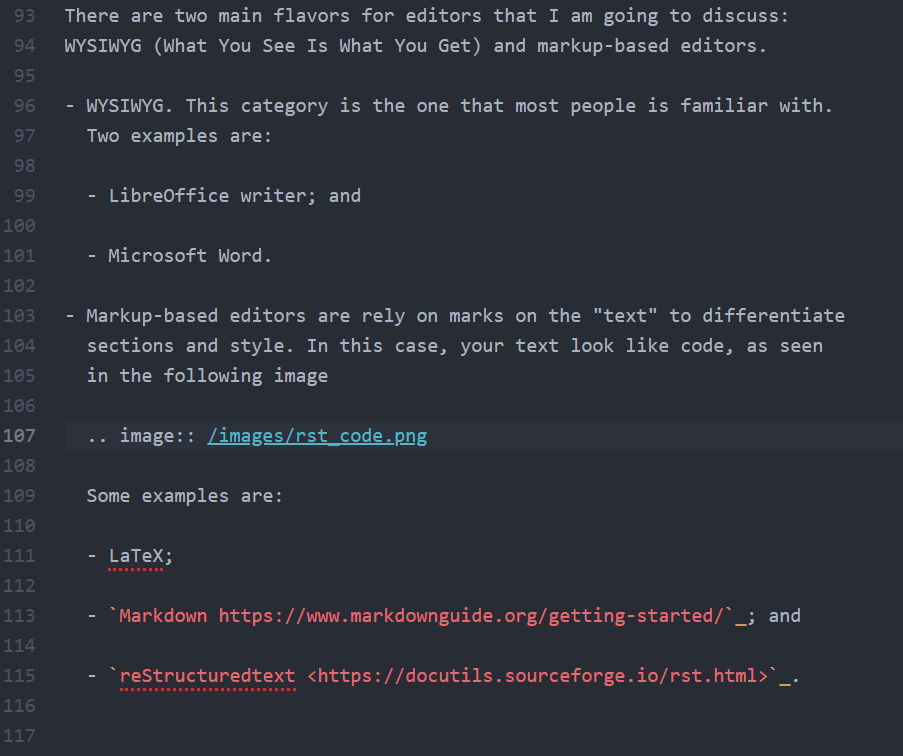
Duplicando un gráfico de la función Hankel de Abramowitz y Stegun
Recientemente, tuve una discusión en clase sobre las soluciones de ecuaciones diferenciales parciales y cómo la visualización jugó un papel importante mucho antes de que las computadoras digitales fueran omnipresentes. También hablamos sobre el Manual de Funciones Matemáticas o Abramowitz y Stegun [1], como se le conoce comúnmente.
Afortunadamente, John D. Cook replicó el siguiente gráfico de Abramowitz y Stegun en su blog utilizando Mathematica. Aunque esta figura fue publicada originalmente en [2].
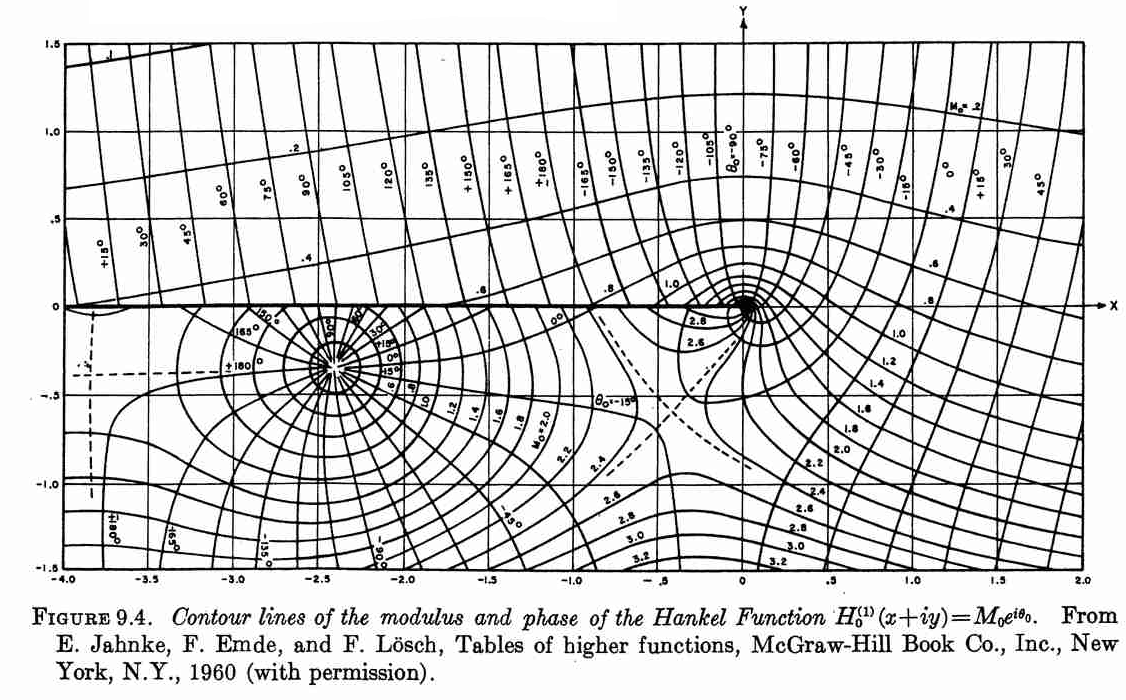
Entonces, intenté replicar esta figura usando Matplotlib.
El siguiente gráfico es el resultado de usar la función contour en el módulo
y la fase de la función de Hankel.

Esto se obtuvo con el siguiente código.
import numpy as np import matplotlib.pyplot as plt from scipy.special import hankel1 y, x = np.mgrid[-1.5:1.5:2500j, -4:2:5000j] z = x + 1j*y H = hankel1(0, z) abs_H = np.abs(H) arg_H = np.rad2deg(np.angle(H)) fig, ax = plt.subplots(figsize=(12, 6)) plt.contour(x, y, abs_H, 20, colors="black") plt.contour(x, y, arg_H, 30, colors="#757575") plt.xticks(np.arange(-4, 2.5, 0.5)) plt.yticks(np.arange(-1.5, 2, 0.5)) plt.xlabel("Real axis") plt.ylabel("Imaginary axis") plt.grid("True") plt.axis("image") plt.savefig("abramowitz_stegun-hankel-0.svg", bbox_inches="tight") plt.show()
Existen algunos problemas con el salto a través de la parte negativa de la línea real. Podemos aplicar una máscara con el siguiente código:
Además, tenemos algunos problemas alrededor de ±180° que corresponden al mismo valor de fase, pero el algoritmo de contorno falla—quizás exista una variante de los marching square que permita trabajar con datos periódicos—. Para solucionar este problema, apliqué el siguiente truco:
Y obtenemos la siguiente figura.

Nos faltan las etiquetas que muestran el valor de algunas curvas de nivel. Si lo hacemos automáticamente, obtenemos la siguiente figura.

Para obtener una figura más cercana a la original, Matplotlib tiene un
parámetro opcional
llamado manual que permite al usuario colocar las
etiquetas de los contornos manualmente.
La siguiente figura se acerca más al original.

El siguiente bloque de código permite obtener la versión final. Puedes descargarlo aquí
import numpy as np import matplotlib.pyplot as plt from scipy.special import hankel1 #%% Data y, x = np.mgrid[-1.5:1.5:2500j, -4:2:5000j] z = x + 1j*y H = hankel1(0, z) abs_H = np.abs(H) abs_H[(x < 0) * (np.abs(y) < 0.01)] = np.nan levels_abs = np.arange(0.2, 3.3, 0.2) arg_H = np.rad2deg(np.angle(H)) arg_H[(x < 0) * (np.abs(y) < 0.01)] = np.nan arg_H[arg_H < -179] += 360 arg_H[arg_H < -178] = np.nan levels_arg = np.arange(-165, 181, 15) #%% Plots setup labels = True manual_labels = True #%% Ploting fig, ax = plt.subplots(figsize=(12, 6)) # Jump line plt.plot([-4, 0], [0, 0], color="black", linewidth=3, zorder=3) # Contours abs_contours = plt.contour(x, y, abs_H, levels_abs, colors="black", linestyles="solid", zorder=4) arg_contours = plt.contour(x, y, arg_H, levels_arg, colors="#757575", linestyles="solid", zorder=6) # Figure details plt.xticks(np.arange(-4, 2.5, 0.5)) plt.yticks(np.arange(-1.5, 2, 0.5)) plt.xlabel("Real axis") plt.ylabel("Imaginary axis") plt.grid("True", color="#BDBDBD", zorder=3) plt.axis("image") # Labels if labels: ax.clabel(abs_contours, levels_abs, fontsize=8, fmt="%.1f", use_clabeltext=True, manual=manual_labels, zorder=5) ax.clabel(arg_contours, levels_arg, fontsize=8, fmt="%d°", colors="#757575", use_clabeltext=True, manual=manual_labels, zorder=6) plt.savefig("abramowitz_stegun-hankel-manual.svg", bbox_inches="tight") plt.show()