Skip to main content

Nicolás' blog

Using Wolfram Language in Jupyter: A free alternative to Mathematica

Nicolás Guarín-Zapata

Comments

Also available in:

Español

In this post I am going to describe how to add the Wolfram Language to the Jupyter notebook. This provides a free alternative to Mathematica with, pretty much, the same syntax. The use of the Wolfram Engine is free for non-production as described in their website:

The Free Wolfram Engine for Developers is available for non-production software development.

You can use this product to:

  • develop a product for yourself or your company

  • conduct personal projects at home, at school, at work

  • explore the Wolfram Language for future production projects

Installation

To install you should do the following steps:

  • Download Wolfram Engine.

  • Create a Wolfram account, if you don't have one.

  • Execute the installer.

  • Type the following in a terminal

wolframscript

and you should be asked for your email and password.

After that you should be in a terminal and see the following

Wolfram Engine activated. See https://www.wolfram.com/wolframscript/ for more information.
Wolfram Language 12.2.0 Engine for Linux x86 (64-bit)
Copyright 1988-2021 Wolfram Research, Inc.

And we can try that it is working

In[1]:= $Version

Out[1]= 12.2.0 for Linux x86 (64-bit) (January 7, 2021)

In[2]:= Integrate[1/(1 + x^2), x]

Out[2]= ArcTan[x]

Now we need to install WolframLanguageForJupyter. For that we can type the following in a terminal

git clone https://github.com/WolframResearch/WolframLanguageForJupyter.git

cd WolframLanguageForJupyter/

./configure-jupyter.wls add

To test that it is installed we can type the following in a terminal

jupyter kernelspec list

and it should have an output that includes a line similar to the following

wolframlanguage12.   /home/nicoguaro/.local/share/jupyter/kernels/wolframlanguage12.2

Or we could also try with

jupyter notebook

and see the following in the kernel menu.

Kernel menu after installing WolframLanguageForJupyter.

Test drive

I tested some of the capabilities and you can download the notebook or see a static version here.

Let's compute the integral

\begin{equation*} \int \frac{1}{1 + x^3}\mathrm{d}x\, . \end{equation*} 
sol:= Integrate[1/(1 + x^3), x]
TeXForm[sol]
\begin{equation*} -\frac{1}{6} \log \left(x^2-x+1\right)+\frac{1}{3} \log (x+1)+\frac{\tan^{-1}\left(\frac{2 x-1}{\sqrt{3}}\right)}{\sqrt{3}} \end{equation*}

And make a 3D plot.

fun:= Sin[Sqrt[x^2 + y^2]]/Sqrt[x^2 + y^2]
Plot3D[fun, {x, -5*Pi, 5*Pi}, {y, -5*Pi, 5*Pi},
    PlotPoints -> 100, BoxRatios -> {1, 1, 0.2},
    PlotRange -> All]
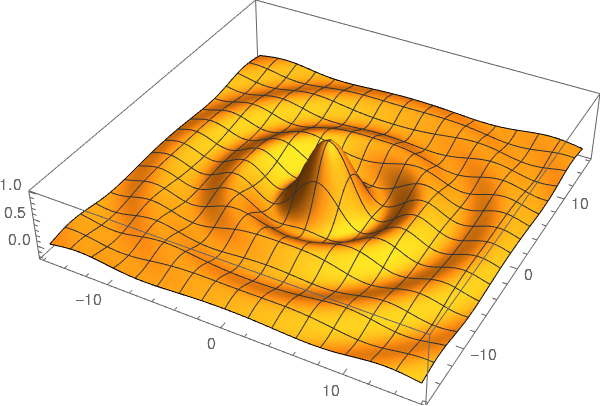
3D plot in the notebook.

In this case we don't have an interactive image. This is still not implemented, but if you are interested there is an open issue about it in GitHub.

Comments

Comments powered by Disqus