Reto de métodos numéricos: resumen

Nicolás Guarín-Zapata

2017-11-14 11:22

Durante octubre (2017) escribí un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tenía experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Resumen

Esta publicación resume el reto. Para ver el código fuente pueden remitirse al repositorio.

El veredicto

Ya que el reto es conmigo mismo, y el propósito era aprender algo de Julia, el veredicto es: exitoso. Sin embargo, fallé en el día 26 con el Método de Elementos de Frontera.

La lista de métodos

Día	Método numérico
01	Bisección
02	Regula falsi
03	Newton
04	Newton multivariable
05	Broyden
06	Descenso del gradiente
07	Nelder-Mead
08	Newton para optimización
09	Interpolación de Lagrange
10	Interpolación de Lagrange con muestreo de Lobatto
11	Interpolación de Lagrange con matriz de Vandermonde
12	Interpolación de Hermite
13	Interpolación spline
14	Cuadratura trapezoidal
15	Cuadratura de Simpson
16	Cuadratura de Clenshaw-Curtis
17	Integración de Euler
18	Integración de Runge-Kutta
19	Integración de Verlet
20	Método del disparo
21	Diferencias finitas con método de Jacobi
22	Diferencias finitas para valores propios
23	Método de Ritz
24	Elementos finitos en 1D
25	Elementos finitos en 2D
26	Método de elementos de frontera
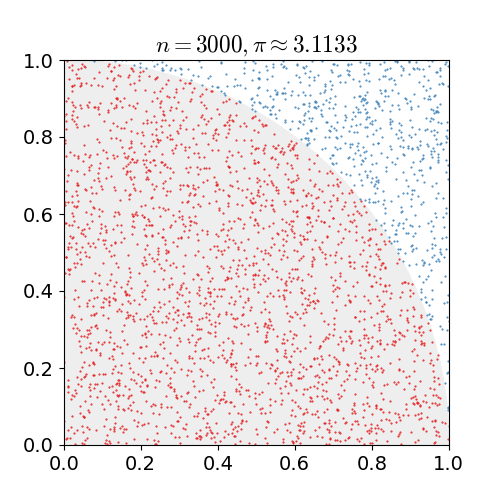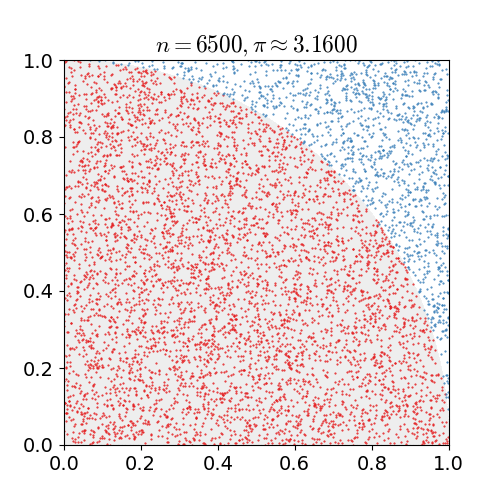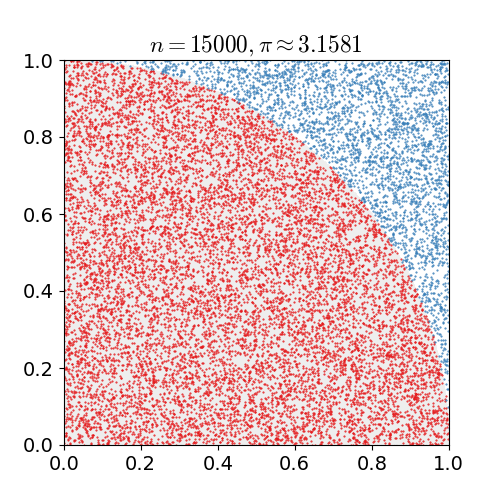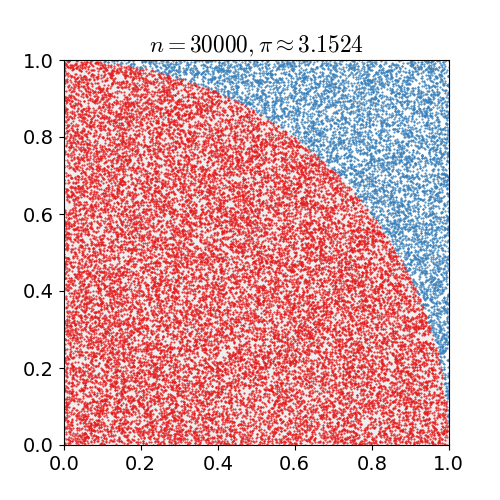
27	Integración Monte-Carlo
28	Factorización LU factorization
29	Factorización de Cholesky
30	Gradiente conjugado
31	Elementos finitos con solucionador

Conclusiones

Este era un ejercicio de kata de código para aprender algunos detalles sobre Julia para computación científica. Como tal, fue muy útil para mí ensuciarme las manos con Julia.
Implementar el Método de Elementos de Frontera en un día parece algo difícil. Yo ya lo sabía de antemano, pero lo intenté de todas formas … sin éxito.
La sintaxis de Julia está en un punto intermedio entre Python y Matlab. Esto hace que sea fácil de usar, aunque la documentación de algunas paquetes está en una etapa preliminar en este momento.
No volveré a hacer un reto como estos en un rato. Requiere de mucha atención realizarlo.

Reto de métodos numéricos: Día 31

Nicolás Guarín-Zapata

2017-10-31 20:45

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Poniendo todo junto

Hoy, estoy juntando partes, es decir, voy a resolver un sistema de ecuaciones que resulta de elementos finitos usando gradiente conjugado.

A continuación el código.

Python

from __future__ import division, print_function
import numpy as np
import matplotlib.pyplot as plt


def FEM1D(coords, source):
    N = len(coords)
    stiff_loc = np.array([[2.0, -2.0], [-2.0, 2.0]])
    eles = [np.array([cont, cont + 1]) for cont in range(0, N - 1)]
    stiff = np.zeros((N, N))
    rhs = np.zeros(N)
    for ele in eles:
        jaco = coords[ele[1]] - coords[ele[0]]
        rhs[ele] = rhs[ele] + jaco*source(coords[ele])
        for cont1, row in enumerate(ele):
            for cont2, col in enumerate(ele):
                stiff[row, col] = stiff[row, col] +  stiff_loc[cont1, cont2]/jaco
    return stiff, rhs


def conj_grad(A, b, x, tol=1e-8):
    r = b - A.dot(x)
    p = r
    rsq_old = r.dot(r)
    for cont in range(len(b)):
        Ap = A.dot(p)
        alpha = rsq_old / p.dot(Ap)
        x = x + alpha*p
        r = r - alpha*Ap
        rsq_new = r.dot(r)
        if np.sqrt(rsq_new) < tol:
            break
        p = r + (rsq_new / rsq_old) * p
        rsq_old = rsq_new
    return x, cont, np.sqrt(rsq_new)


fun = lambda x: x**3
N_vec = np.logspace(0.5, 3, 50, dtype=int)
err_vec = np.zeros_like(N_vec, dtype=float)
niter_vec = np.zeros_like(N_vec)
plt.figure(figsize=(8, 3))
for cont, N in enumerate(N_vec):
    x = np.linspace(0, 1, N)
    stiff, rhs = FEM1D(x, fun)
    sol = np.zeros(N)
    sol[1:-1], niter, _ = conj_grad(stiff[1:-1, 1:-1], -rhs[1:-1], rhs[1:-1])
    err = np.linalg.norm(sol - x*(x**4 - 1)/20)/np.linalg.norm(x*(x**4 - 1)/20)
    err_vec[cont] = err
    niter_vec[cont] = niter

plt.subplot(121)
plt.loglog(N_vec, err_vec)
plt.xlabel("Number of nodes")
plt.ylabel("Relative error")
plt.subplot(122)
plt.loglog(N_vec, niter_vec)
plt.xlabel("Number of nodes")
plt.ylabel("Number of iterations")
plt.tight_layout()
plt.show()

Julia

using PyPlot


function FEM1D(coords, source)
    N = length(coords)
    stiff_loc = [2.0 -2.0; -2.0 2.0]
    eles = [[cont, cont + 1] for cont in 1:N-1]
    stiff = zeros(N, N)
    rhs = zeros(N)
    for ele in eles
        jaco = coords[ele[2]] - coords[ele[1]]
        rhs[ele] = rhs[ele] + jaco*source(coords[ele])
        stiff[ele, ele] = stiff[ele, ele] +  stiff_loc/jaco
    end
    return stiff, rhs
end


function conj_grad(A, b, x; tol=1e-8)
    r = b - A * x
    p = r
    rsq_old = dot(r, r)
    niter = 1
    for cont = 1:length(b)
        Ap = A * p
        alpha = rsq_old / dot(p, Ap)
        x = x + alpha*p
        r = r - alpha*Ap
        rsq_new = dot(r, r)
        if sqrt(rsq_new) < tol
            break
        end
        p = r + (rsq_new / rsq_old) * p
        rsq_old = rsq_new
        niter += 1
    end
    return x, niter, norm(r)
end



fun(x) = x.^3
N_vec = round.(logspace(0.5, 3, 50))
err_vec = zeros(N_vec)
niter_vec = zeros(N_vec)
figure(figsize=(8, 3))
for (cont, N) in enumerate(N_vec)
    x = linspace(0.0, 1.0,N)
    stiff, rhs = FEM1D(x, fun)
    sol = zeros(N)
    sol[2:end-1], niter, _ = conj_grad(stiff[2:end-1, 2:end-1],
                                -rhs[2:end-1], rhs[2:end-1])
    err = norm(sol - x.*(x.^4 - 1)/20)/norm(x.*(x.^4 - 1)/20)
    err_vec[cont] = err
    niter_vec[cont] = niter
end
subplot(121)
loglog(N_vec, err_vec)
xlabel("Number of nodes")
ylabel("Relative error")
subplot(122)
loglog(N_vec, niter_vec)
xlabel("Number of nodes")
ylabel("Number of iterations")
tight_layout()
show()

En este caso, vamos a analizar el error de la solución como función del número de nodos. Se muestra esto y el número de iteraciones requeridas en el gradiente conjugado.

Reto de métodos numéricos: Día 30

Nicolás Guarín-Zapata

2017-10-30 19:38

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Gradiente conjugado

Hoy tenemos el método del gradiente conjugado. Este método se usa comúnmente para resolver sistemas lineales positivos definidos. En comparación con el descenso del gradiente, escogemos una dirección de descenso que es conjugado con su residual, es decir, es ortogonal con una matriz de ponderación.

A continuación se presenta el código.

Python

from __future__ import division, print_function
import numpy as np


def conj_grad(A, b, x, tol=1e-8):
    r = b - A.dot(x)
    p = r
    rsq_old = r.dot(r)
    for cont in range(len(b)):
        Ap = A.dot(p)
        alpha = rsq_old / p.dot(Ap)
        x = x + alpha*p
        r = r - alpha*Ap
        rsq_new = r.dot(r)
        if np.sqrt(rsq_new) < tol:
            break
        p = r + (rsq_new / rsq_old) * p
        rsq_old = rsq_new
    return x, cont, np.sqrt(rsq_new)


N = 1000
A = -np.diag(2*np.ones(N)) + np.diag(np.ones(N-1), -1) +\
    np.diag(np.ones(N-1), 1)
b = np.ones(N)
x0 = np.ones(N)
x, niter, accu = conj_grad(A, b, x0)

Julia

function conj_grad(A, b, x; tol=1e-8)
    r = b - A * x
    p = r
    rsq_old = dot(r, r)
    niter = 1
    for cont = 1:length(b)
        Ap = A * p
        alpha = rsq_old / dot(p, Ap)
        x = x + alpha*p
        r = r - alpha*Ap
        rsq_new = dot(r, r)
        if sqrt(rsq_new) < tol
            break
        end
        p = r + (rsq_new / rsq_old) * p
        rsq_old = rsq_new
        niter += 1
    end
    return x, niter, norm(r)
end


N = 1000
A = -diagm(2*ones(N)) + diagm(ones(N-1), -1) + diagm(ones(N-1), 1)
b = ones(N)
x0 = ones(N)
x, niter, accu = conj_grad(A, b, x0)

En este caso, vamos a probar el método con una matriz que viene de una discretización de una derivada de segundo orden usando diferencias finitas.

Comparación Python/Julia

Respecto al número de líneas tenemos: 27 en Python y 27 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia.

Para Python:

%timeit conj_grad(A, b, x0)

con resultado

10 loops, best of 3: 107 ms per loop

Para Julia:

@benchmark conj_grad(A, b, x0)

con resultado

BenchmarkTools.Trial:
  memory estimate:  27.13 MiB
  allocs estimate:  3501
  --------------
  minimum time:     128.477 ms (0.54% GC)
  median time:      294.407 ms (0.24% GC)
  mean time:        298.208 ms (0.30% GC)
  maximum time:     464.223 ms (0.30% GC)
  --------------
  samples:          17
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 2 veces más rápido que el de Julia.

Reto de métodos numéricos: Día 29

Nicolás Guarín-Zapata

2017-10-29 21:10

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Descomposición de Cholesky

Hoy tenemos la descomposición de Cholesky. Es una factorización de una matriz hermítica, positiva definita en matrices triangulares inferior y superior. La diferencia principal con la descomposición LU es que la matriz inferior es la transpuesta hermítica de la superior.

A continuación se presenta el código.

Python

from __future__ import division, print_function
import numpy as np


def cholesky(mat):
    m, _ = mat.shape
    mat = mat.copy()
    for col in range(m):
        print(mat[col, col] -
               mat[col, 0:col].dot(mat[col, 0:col]))
        mat[col, col] = np.sqrt(mat[col, col] -
               mat[col, 0:col].dot(mat[col, 0:col]))
        for row in range(col + 1, m):
            mat[row, col] = (mat[row, col] -
               mat[row, 0:col].dot(mat[col, 0:col]))/mat[col, col]
    for row in range(1, m):
        mat[0:row, row] = 0
    return mat


A = np.array([
    [4, -1, 1],
    [-1, 4.25, 2.75],
    [1, 2.75, 3.5]], dtype=float)
B = cholesky(A)

Julia

function cholesky(mat)
    m, _ = size(mat)
    mat = copy(mat)
    for col = 1:m
        mat[col, col] = sqrt(mat[col, col] -
            dot(mat[col, 1:col-1], mat[col, 1:col-1]))
        for row = col + 1:m
            mat[row, col] = (mat[row, col] -
               dot(mat[row, 1:col-1], mat[col, 1:col-1]))/mat[col, col]
        end
    end
    for row = 2:m
        mat[1:row-1, row] = 0
    end
    return mat
end


A = [4 -1 1;
    -1 4.25 2.75;
    1 2.75 3.5]
B = cholesky(A)

Como ejemplo tenemos la siguiente matriz

\begin{equation*} A = \begin{bmatrix} 4 &-1 &1\\ -1 &4.25 &2.75\\ 1 &2.75 &3.5 \end{bmatrix} \end{equation*}

Y la respuesta en ambos códigos es

2.0  0.0  0.0
-0.5  2.0  0.0
0.5  1.5  1.0

Comparación Python/Julia

Respecto al número de líneas tenemos: 23 en Python y 22 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia.

Para Python:

%timeit cholesky(np.eye(100))

con resultado

100 loops, best of 3: 13 ms per loop

Para Julia:

@benchmark cholesky(eye(100))

con resultado

BenchmarkTools.Trial:
  memory estimate:  4.01 MiB
  allocs estimate:  20303
  --------------
  minimum time:     1.010 ms (0.00% GC)
  median time:      1.136 ms (0.00% GC)
  mean time:        1.370 ms (17.85% GC)
  maximum time:     4.652 ms (40.37% GC)
  --------------
  samples:          3637
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 10 veces más lento que el de Julia.

Reto de métodos numéricos: Día 28

Nicolás Guarín-Zapata

2017-10-28 17:02

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Factorización LU

Hoy tenemos la descomposición LU. Este es la factorización de una matriz en su formas triangulares inferior (L) y superior (U). Básicamente, almacena cada uno de los pasos de una eliminación gaussiana en matrices.

A continuación el código.

Python

from __future__ import division, print_function
import numpy as np


def LU(mat):
    m, _ = mat.shape
    mat = mat.copy()
    for col in range(0, m - 1):
        for row in range(col + 1, m):
            if mat[row, col] != 0.0:
                lam = mat[row, col]/mat[col, col]
                mat[row, col + 1:m] = mat[row, col + 1:m] -\
                                      lam * mat[col, col + 1:m]
                mat[row, col] = lam
    return mat


A = np.array([
    [1, 1, 0, 3],
    [2, 1, -1, 1],
    [3, -1, -1, 2],
    [-1, 2, 3, -1]], dtype=float)
B = LU(A)

Julia

function LU(mat)
    m, _ = size(mat)
    mat = copy(mat)
    for col = 1:m - 2
        for row = col + 1:m
            if mat[row, col] != 0.0
                lam = mat[row, col]/mat[col, col]
                mat[row, col + 1:m] = mat[row, col + 1:m] -
                                      lam * mat[col, col + 1:m]
                mat[row, col] = lam
            end
        end
    end
    return mat
end


A = [1.0 1.0 0.0 3.0;
    2.0 1.0 -1.0 1.0;
    3.0 -1.0 -1.0 2.0;
    -1.0 2.0 3.0 -1.0]
B = LU(A)

Como un ejemplo tenemos la matriz

\begin{equation*} A = \begin{bmatrix} 1 &1 &0 &3\\ 2 &1 &-1 &1\\ 3 &-1 &-1 &2\\ -1 &2 &3 &-1 \end{bmatrix} = \begin{bmatrix} 1 &1 &0 &0\\ 2 &1 &0 &0\\ 3 &4 &1 &2\\ -1 &-3 &0 &1 \end{bmatrix} \begin{bmatrix} 1 &1 &0 &3\\ 0 &-1 &-1 &-5\\ 0 &0 &3 &13\\ 0 &0 &0 &-13 \end{bmatrix} \end{equation*}

Y, la respuesta en ámbos códigos es

[[  1.,   1.,   0.,   3.],
 [  2.,  -1.,  -1.,  -5.],
 [  3.,   4.,   3.,  13.],
 [ -1.,  -3.,   0., -13.]]

Comparación Python/Julia

Respecto al número de líneas tenemos: 23 en Python y 22 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia.

Para Python:

%timeit LU(np.random.rand(10, 10))

con resultado

1000 loops, best of 3: 303 µs per loop

Para Julia:

@benchmark LU(rand(10, 10))

con resultado

BenchmarkTools.Trial:
  memory estimate:  29.25 KiB
  allocs estimate:  310
  --------------
  minimum time:     9.993 μs (0.00% GC)
  median time:      11.725 μs (0.00% GC)
  mean time:        14.943 μs (15.90% GC)
  maximum time:     3.285 ms (95.64% GC)
  --------------
  samples:          10000
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 30 veces más lento que el de Julia.

Reto de métodos numéricos: Día 27

Nicolás Guarín-Zapata

2017-10-27 21:27

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Integración Monte Carlo

Hoy tenemos la integración Monte Carlo. En donde usamos muestreo aleatorio para calcular una integral numéricamente. Este método es importante cuando tenemos que evaluar integrales multidimensionales ya que las técnicas de cuadratura usuales implican un crecimiento exponencial con el número de puntos de muestreo.

El método cálcula una integral

\begin{equation*} I = \int_\Omega f(x) dx \end{equation*}

donde \(\Omega\) tiene volumen \(V\).

La integral es aproximada como

\begin{equation*} I \approx \frac{V}{N} \sum_{i=1}^{N} f(x_i) \end{equation*}

donde \(x_i\) está distribuido de manera uniforme sobre \(\Omega\).

A continuación se presenta el código.

Python

from __future__ import division, print_function
import numpy as np


def monte_carlo_int(fun, N, low, high, args=()):
    ndims = len(low)
    pts = np.random.uniform(low=low, high=high, size=(N, ndims))
    V = np.prod(np.asarray(high) - np.asarray(low))
    return V*np.sum(fun(pts, *args))/N


def circ(x, rad):
    return 0.5*(1 - np.sign(x[:, 0]**2 + x[:, 1]**2 - rad**2))


N = 1000000
low = [-1, -1]
high = [1, 1]
rad = 1
inte = monte_carlo_int(circ, N, low, high, args=(rad,))

Julia

using Distributions


function monte_carlo_int(fun, N, low, high; args=())
    ndims = length(low)
    pts = rand(Uniform(0, 1), N, ndims)
    for cont = 1:ndims
        pts[:, cont] = pts[:, cont]*(high[cont] - low[cont]) + low[cont]
    end
    V = prod(high - low)
    return V*sum(fun(pts, args...))/N
end


function circ(x, rad)
    return 0.5*(1 - sign.(x[:, 1].^2 + x[:, 2].^2 - rad^2))
end


N = 1000000
low = [-1, -1]
high = [1, 1]
rad = 1
inte = monte_carlo_int(circ, N, low, high, args=(rad,))

Una de los ejemplos más comunes es el cálculo de \(\pi\), esto se ilustra en la siguiente animación.

Comparación Python/Julia

Respecto al número de líneas tenemos: 20 en Python y 24 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia.

Para Python:

%timeit monte_carlo_int(circ, N, low, high, args=(rad,))

con resultado

10 loops, best of 3: 53.2 ms per loop

Para Julia:

@benchmark monte_carlo_int(circ, N, low, high, args=(rad,))

con result

BenchmarkTools.Trial:
  memory estimate:  129.70 MiB
  allocs estimate:  46
  --------------
  minimum time:     60.131 ms (5.15% GC)
  median time:      164.018 ms (55.64% GC)
  mean time:        204.366 ms (49.50% GC)
  maximum time:     357.749 ms (64.04% GC)
  --------------
  samples:          25
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 3 veces más rápido que el de Julia.

Reto de métodos numéricos: Día 26

Nicolás Guarín-Zapata

2017-10-26 19:15

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Método de elementos de frontera

Hoy tenemos el método de elementos de frontera, o, un intento de él. Queremos resolver la ecuación

\begin{equation*} \nabla^2 u = -f(x) \end{equation*}

con

\begin{equation*} u(x) = g(x),\quad \forall (x, y)\in \partial \Omega \end{equation*}

Para este método, necesitamos la repreentación integral de la ecuación, que en este caso es

\begin{equation*} u(\xi) = \int_{S} [u(x) F(x, \xi) - q(x)G(x, \xi)]dS(x) + \int_{V} f(x) G(x, \xi) dV(x) \end{equation*}

con

\begin{equation*} G(x,\xi)= -\frac{1}{2\pi}\ln|x- \xi| \end{equation*}

y

\begin{equation*} F(x,\xi) = -\frac{1}{2\pi |x- \xi|^2}(x - \xi)\cdot\hat{n} \end{equation*}

Entonces, podemos formar el sistema de ecuaciones

\begin{equation*} [G]\{q\} = [F]\{u\}\, , \end{equation*}

Que obtenemos de discretizar la frontera. Si tomamos variables constantes a lo largo de la discretización, las integrales se pueden calcular analíticamente

\begin{equation*} G_{nm} = -\frac{1}{2\pi}\left[r \sin\theta\left(\ln|r| - 1\right) + \theta r\cos\theta\right]^{\theta_B, r_B}_{\theta_A, r_A} \end{equation*}

y

\begin{equation*} F_{nm} = \left[\frac{\theta}{2\pi}\right]^{\theta_B}_{\theta_A} \end{equation*}

para \(n\) y \(m\) en diferentes elementos, y los subíndices \(A,B\) se refieren a los puntos finales del elemento a evaluar. Para los términos en la diagonal las integrales son

\begin{equation*} G_{nn} = -\frac{L}{2\pi}\left(\ln\left\vert\frac{L}{2}\right\vert - 1\right) \end{equation*}

y

\begin{equation*} F_{nn} = - \frac{1}{2\pi} \end{equation*}

con \(L\), el tamaño del elemento.

A continuación se muestra el código de Python. En este caso, no tuve éxito en hacer que el código funcionara.

from __future__ import division, print_function
import numpy as np
from numpy import log, sin, cos, arctan2, pi, mean, arctan
from numpy.linalg import norm, solve
import matplotlib.pyplot as plt


def assem(coords, elems):
    nelems = elems.shape[0]
    Gmat = np.zeros((nelems, nelems))
    Fmat = np.zeros((nelems, nelems))
    for ev_cont, elem1 in enumerate(elems):
        print(coords[elem1[0]], coords[elem1[1]])
        for col_cont, elem2 in enumerate(elems):
            pt_col = mean(coords[elem2], axis=0)
            if ev_cont == col_cont:
                L = norm(coords[elem1[1]] - coords[elem1[0]])
                Gmat[ev_cont, ev_cont] = - L/(2*pi)*(log(L/2) - 1)
                Fmat[ev_cont, ev_cont] = - 0.5
            else:
                Gij, Fij = influence_coeff(elem1, coords, pt_col)
                Gmat[ev_cont, col_cont] = Gij
                Fmat[ev_cont, col_cont] = Fij
    return Gmat, Fmat


def influence_coeff(elem, coords, pt_col):
    r_A = coords[elem[0]] - pt_col
    r_B = coords[elem[1]] - pt_col
    theta_A = arctan2(r_A[1], r_A[0])
    theta_B = arctan2(r_B[1], r_B[0])
    G_coeff = r_B[1]*(log(norm(r_B)) - 1) + theta_B*r_B[0] -\
              (r_A[1]*(log(norm(r_A)) - 1) + theta_A*r_A[0])
    F_coeff = theta_B - theta_A
    return -G_coeff/(2*pi), F_coeff/(2*pi)


def eval_sol(ev_coords, coords):
    nelems = elems.shape[0]
    Gmat = np.zeros((nelems, nelems))
    Fmat = np.zeros((nelems, nelems))
    for ev_cont, elem1 in enumerate(elems):
        L = norm(coords[elem1[1]] - coords[elem1[0]])
        for col_cont, elem2 in enumerate(elems):
            pt_col = mean(coords[elem2], axis=0)
            if ev_cont == col_cont:
                Gmat[ev_cont, ev_cont] = - L/(2*pi)*(log(L/2) - 1)
                Fmat[ev_cont, ev_cont] = - 0.5
            else:
                Gmat[ev_cont, col_cont], Fmat[ev_cont, col_cont] = \
                    influence_coeff(elem1, coords, pt_col)

nelems = 3
rad = 1.0
theta =  np.linspace(0, 2*pi, nelems, endpoint=False)
coords = rad * np.vstack((cos(theta), sin(theta))).T
elems = np.array([[cont, (cont + 1)%nelems] for cont in range(nelems)])
Gmat, Fmat = assem(coords, elems)
u_boundary = np.ones_like(theta)
q_boundary = solve(Gmat, Fmat.dot(u_boundary))

Reto de métodos numéricos: Día 25

Nicolás Guarín-Zapata

2017-10-25 21:41

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Método de elementos finitos

Hoy tenemos el método de elementos finitos para resolver la ecuación:

\begin{equation*} \nabla^2 u = -f(x) \end{equation*}

con

\begin{equation*} u(\sqrt{3}, 1) = 0 \end{equation*}

Como en el método de Ritz formamos un funcional que es equivalente a la ecuación diferencial, proponemos una aproximación que es una combinación lineal de funciones base y encontramos el mejor conjunto de coeficientes para esta combinación. La mejor solución se encuentra minimizando el funcional.

El funcional para este ecuación diferencial es

\begin{equation*} \Pi[u] = -\int_\Omega \left(\nabla u\right)^2 d\Omega -\int_\Omega u f(x) d\Omega \end{equation*}

Usando triángulos lineales, las matrices de rigidez son

\begin{equation*} K_\text{local} = \frac{1}{2|J|} \begin{bmatrix} 2 & -1 &1\\ -1 & 1 &0\\ -1 & 0 &1\\ \end{bmatrix} \end{equation*}

y

\begin{equation*} b_\text{local} = -|J| f(x_m) \mathbf{1}_3\, , \end{equation*}

donde \(|J|\) es el determinante jacobiano de la transformación y \(x_m\) es el centroide del triángulo. Me estoy saltando muchos detalles respecto al ensamblaje; sería muy costoso describir el proceso completo.

Vamos a resolver el problema en una malla de 6 triángulos que forman un hexágono regular.

A continuación se presenta el código.

Python

from __future__ import division, print_function
import numpy as np
import matplotlib.pyplot as plt

def assem(coords, elems, source):
    ncoords = coords.shape[0]
    stiff = np.zeros((ncoords, ncoords))
    rhs = np.zeros((ncoords))
    for el_cont, elem in enumerate(elems):
        stiff_loc, jaco = local_stiff(coords[elem])
        rhs[elem] += jaco*np.mean(source[elem])
        for row in range(3):
            for col in range(3):
                row_glob, col_glob = elem[row], elem[col]
                stiff[row_glob, col_glob] += stiff_loc[row, col]
    return stiff, rhs


def local_stiff(coords):
    dHdr = np.array([[-1, 1, 0], [-1, 0, 1]])
    jaco = dHdr.dot(coords)
    stiff = 0.5*np.array([[2, -1, -1], [-1, 1, 0], [-1, 0, 1]])
    return stiff/np.linalg.det(jaco), np.linalg.det(jaco)


sq3 = np.sqrt(3)
coords = np.array([
        [sq3, -1],
        [0, 0],
        [2*sq3, 0],
        [0, 2],
        [2*sq3, 2],
        [sq3, 3],
        [sq3, 1]])
elems = np.array([
        [1, 0, 6],
        [0, 2, 6],
        [2, 4, 6],
        [4, 5, 6],
        [5, 3, 6],
        [3, 1, 6]])
source = -np.ones(7)
stiff, rhs = assem(coords, elems, source)
free = range(6)
sol = np.linalg.solve(stiff[np.ix_(free, free)], rhs[free])
sol_c = np.zeros(coords.shape[0])
sol_c[free] = sol
plt.tricontourf(coords[:, 0], coords[:, 1], sol_c, cmap="hot")
plt.colorbar()
plt.axis("image")
plt.show()

Julia

using PyPlot


function assem(coords, elems, source)
    ncoords = size(coords)[1]
    nelems = size(elems)[1]
    stiff = zeros(ncoords, ncoords)
    rhs = zeros(ncoords)
    for el_cont = 1:nelems
        elem = elems[el_cont, :]
        stiff_loc, jaco = local_stiff(coords[elem, :])
        rhs[elem] += jaco*mean(source[elem])
        for row = 1:3
            for col = 1:3
                row_glob = elem[row]
                col_glob = elem[col]
                stiff[row_glob, col_glob] += stiff_loc[row, col]
            end
        end
    end
    return stiff, rhs
end


function local_stiff(coords)
    dHdr = [-1 1 0; -1 0 1]
    jaco = dHdr * coords
    stiff = 0.5*[2 -1 -1; -1 1 0; -1 0 1]
    return stiff/det(jaco), det(jaco)
end


sq3 = sqrt(3)
coords =[sq3 -1;
        0 0;
        2*sq3 0;
        0 2;
        2*sq3 2;
        sq3 3;
        sq3 1]
elems =[2 1 7;
        1 3 7;
        3 5 7;
        5 6 7;
        6 4 7;
        4 2 7]
source = -ones(7)
stiff, rhs = assem(coords, elems, source)
free = 1:6
sol = stiff[free, free] \ rhs[free]
sol_c = zeros(size(coords)[1])
sol_c[free] = sol
tricontourf(coords[:, 1], coords[:, 2], sol_c, cmap="hot")
colorbar()
axis("image")
show()

En ambos casos tenemos el mismo resultado.

Aproximación por el método de elementos finitos.

Comparación Python/Julia

Respecto al número de líneas tenemos: 51 en Python y 56 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia. Para la comparación solo estamos considerando el tiempo que toma formar las matrices.

Para Python:

%timeit assem(coords, elems, source)

con resultado

1000 loops, best of 3: 671 µs per loop

Para Julia:

@benchmark assem(coords, elems, source)

con resultado

BenchmarkTools.Trial:
  memory estimate:  13.30 KiB
  allocs estimate:  179
  --------------
  minimum time:     7.777 μs (0.00% GC)
  median time:      8.934 μs (0.00% GC)
  mean time:        10.810 μs (14.54% GC)
  maximum time:     797.432 μs (95.85% GC)
  --------------
  samples:          10000
  evals/sample:     4

En este caso, podemos decir que el código de Python es alrededor de 70 veces más lento que el de Julia.

Reto de métodos numéricos: Día 24

Nicolás Guarín-Zapata

2017-10-24 15:17

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Método de elementos finitos

Hoy tenemos el método de elementos finitos para resolver la ecuación:

\begin{equation*} \frac{d^2 u}{dx^2} = f(x) \end{equation*}

con

\begin{equation*} u(0) = u(1) = 0 \end{equation*}

Como en el método de Ritz formamos un funcional que es equivalente a la ecuación diferencial, proponemos una aproximación que es una combinación lineal de funciones base y encontramos el mejor conjunto de coeficientes para esta combinación. La mejor solución se encuentra minimizando el funcional.

El funcional para este ecuación diferencial es

\begin{equation*} \Pi[u] = -\int_{0}^{1} \left(\frac{d u}{d x}\right)^2 dx -\int_{0}^{1} u f(x) dx \end{equation*}

La diferencia principal es que usamos interpolación por tramos como funciones base,

\begin{equation*} \hat{u}(x) = \sum_{n=0}^{N} u_n N_n(x)\, , \end{equation*}

Esto lleva al siguiente sistema de ecuaciones

\begin{equation*} [K]\{\mathbf{c}\} = \{\mathbf{b}\} \end{equation*}

donde las matrices de rigidez locales están dadas por

\begin{equation*} K_\text{local} = \frac{1}{|J|}\begin{bmatrix} 2 & -2\\ -2 &2\end{bmatrix} \end{equation*}

y

\begin{equation*} b_\text{local} = -|J|\begin{bmatrix} f(x_m)\\ f(x_{n})\end{bmatrix}\, , \end{equation*}

donde \(|J|\) es el determinante jacobian de la transformación. Me estoy saltando muchos detalles respecto al ensamblaje; sería muy costoso describir el proceso completo.

Probaremos la implementación con la función \(f(x) = x^3\), que lleva a la solución .. math:

u(x) = \frac{x (x^4 - 1)}{20}

A continuacón se presenta el código.

Python

from __future__ import division, print_function
import numpy as np
import matplotlib.pyplot as plt


def FEM1D(coords, source):
    N = len(coords)
    stiff_loc = np.array([[2.0, -2.0], [-2.0, 2.0]])
    eles = [np.array([cont, cont + 1]) for cont in range(0, N - 1)]
    stiff = np.zeros((N, N))
    rhs = np.zeros(N)
    for ele in eles:
        jaco = coords[ele[1]] - coords[ele[0]]
        rhs[ele] = rhs[ele] + jaco*source(coords[ele])
        for cont1, row in enumerate(ele):
            for cont2, col in enumerate(ele):
                stiff[row, col] = stiff[row, col] +  stiff_loc[cont1, cont2]/jaco
    return stiff, rhs


N = 100
fun = lambda x: x**3
x = np.linspace(0, 1, N)
stiff, rhs = FEM1D(x, fun)
sol = np.zeros(N)
sol[1:-1] = np.linalg.solve(stiff[1:-1, 1:-1], -rhs[1:-1])


#%% Plotting
plt.figure(figsize=(4, 3))
plt.plot(x, sol)
plt.plot(x, x*(x**4 - 1)/20, linestyle="dashed")
plt.xlabel(r"$x$")
plt.ylabel(r"$y$")
plt.legend(["FEM solution", "Exact solution"])
plt.tight_layout()
plt.show()

Julia

using PyPlot


function FEM1D(coords, source)
    N = length(coords)
    stiff_loc = [2.0 -2.0; -2.0 2.0]
    eles = [[cont, cont + 1] for cont in 1:N-1]
    stiff = zeros(N, N)
    rhs = zeros(N)
    for ele in eles
        jaco = coords[ele[2]] - coords[ele[1]]
        rhs[ele] = rhs[ele] + jaco*source(coords[ele])
        stiff[ele, ele] = stiff[ele, ele] +  stiff_loc/jaco
    end
    return stiff, rhs
end


N = 100
fun(x) = x.^3
x = linspace(0, 1, N)
stiff, rhs = FEM1D(x, fun)
sol = zeros(N)
sol[2:end-1] = -stiff[2:end-1, 2:end-1]\rhs[2:end-1]


#%% Plotting
figure(figsize=(4, 3))
plot(x, sol)
plot(x, x.*(x.^4 - 1)/20, linestyle="dashed")
xlabel(L"$x$")
ylabel(L"$y$")
legend(["FEM solution", "Exact solution"])
tight_layout()
show()

Ambos presentan el mismo resultado que se ve a continuación.

Comparación Python/Julia

Respecto al número de líneas tenemos: 37 en Python y 35 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia. Para la comparación solo estamos considerando el tiempo que toma formar las matrices.

Para Python:

%timeit FEM1D(x, fun)

con resultado

100 loops, best of 3: 2.15 ms per loop

Para Julia:

@benchmark FEM1D(x, fun)

con resultado

BenchmarkTools.Trial:
  memory estimate:  183.73 KiB
  allocs estimate:  1392
  --------------
  minimum time:     60.045 μs (0.00% GC)
  median time:      70.445 μs (0.00% GC)
  mean time:        98.276 μs (25.64% GC)
  maximum time:     4.269 ms (96.70% GC)
  --------------
  samples:          10000
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 30 veces más lento que el de Julia.

Reto de métodos numéricos: Día 23

Nicolás Guarín-Zapata

2017-10-23 20:30

Comentarios

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Método de Ritz

Hoy tenemos el método de Ritz para resolver la ecuación:

\begin{equation*} \frac{d^2 u}{dx^2} = f(x) \end{equation*}

con

\begin{equation*} u(0) = u(1) = 0 \end{equation*}

El método consiste en formar un funcional que es equivalente a la ecuación diferencial, proponer una aproximación como una combinación lineal de un conjunto de funciones base y encontrar el mejor conjunto de coeficientes para esta combinación. Este mejor solución se encuentra minimizando el funcional.

El funcional para esta ecuación diferencial es

\begin{equation*} \Pi[u] = -\int_{0}^{1} \left(\frac{d u}{d x}\right)^2 dx -\int_{0}^{1} u f(x) dx \end{equation*}

En este caso, estamos usando la aproximación

\begin{equation*} \hat{u}(x) = x (1 - x)\sum_{n=0}^{N} c_n x^n\, , \end{equation*}

en donde escogimos el factor \(x (1 - x)\) para forzar que las funciones satisfagan las condiciones de frontera. El funcional aproximado es

\begin{align*} \Pi[\hat{u}] = -\sum_{n=0}^{N} \sum_{m=0}^{N} c_n c_m \left[\frac{2 + 2m + 2n + 2mn}{(n + m + 1)(n + m + 2)(n + m +3)}\right] -\\ \sum_{n=0}^{N} c_n\int_{0}^{1} x^{n + 1}(1 - x) f(x) dx \end{align*}

en donde, en general, necesitamos realizar una integración numérica para el segundo término.

Minimizando el funcional

\begin{equation*} \frac{\partial \Pi[\hat{u}]}{\partial c_m} = 0\, , \end{equation*}

obtenmos el siguiente sistema de ecuaciones

\begin{equation*} [K]\{\mathbf{c}\} = \{\mathbf{b}\} \end{equation*}

con

\begin{equation*} K_{mn} = \frac{2 + 2m + 2n + 2mn}{(n + m + 1)(n + m + 2)(n + m +3)} \end{equation*}

y

\begin{equation*} b_m = -\int_{0}^{1} x^{m + 1}(1 - x) f(x) dx\, . \end{equation*}

Probaremos la implementación con la función \(f(x) = x^3\), que lleva a la solución

\begin{equation*} u(x) = \frac{x (x^4 - 1)}{20} \end{equation*}

A continuación se presenta el código.

Python

from __future__ import division, print_function
import numpy as np
from scipy.integrate import quad
from scipy.linalg import solve
import matplotlib.pyplot as plt


def ritz(N, source):
    stiff_mat = np.zeros((N, N))
    rhs = np.zeros((N))
    for row in range(N):
        for col in range(N):
            numer = (2 + 2*row + 2*col + 2*row*col)
            denom = (row + col + 1) * (row + col + 2) * (row + col + 3)
            stiff_mat[row, col] = numer/denom
        fun = lambda x: x**(row + 1)*(1 - x)*source(x)
        rhs[row], _ = quad(fun, 0, 1)
    return stiff_mat, rhs


N = 2
source = lambda x: x**3
mat, rhs = ritz(N, source)
c = solve(mat, -rhs)
x = np.linspace(0, 1, 100)
y = np.zeros_like(x)
for cont in range(N):
    y += c[cont]*x**(cont + 1)*(1 - x)

#%% Plotting
plt.figure(figsize=(4, 3))
plt.plot(x, y)
plt.plot(x, x*(x**4 - 1)/20, linestyle="dashed")
plt.xlabel(r"$x$")
plt.ylabel(r"$y$")
plt.legend(["Ritz solution", "Exact solution"])
plt.tight_layout()
plt.show()

Julia

using PyPlot


function ritz(N, source)
    stiff_mat = zeros(N, N)
    rhs = zeros(N)
    for row in 0:N-1
        for col in 0:N-1
            numer = (2 + 2*row + 2*col + 2*row*col)
            denom = (row + col + 1) * (row + col + 2) * (row + col + 3)
            stiff_mat[row + 1, col + 1] = numer/denom
        end
        fun(x) = x^(row + 1)*(1 - x)*source(x)
        rhs[row + 1], _  = quadgk(fun, 0, 1)
    end
    return stiff_mat, rhs
end


N = 2
source(x) = x^3
mat, rhs = ritz(N, source)
c = -mat\rhs
x = linspace(0, 1, 100)
y = zeros(x)
for cont in 0:N - 1
    y += c[cont + 1]*x.^(cont + 1).*(1 - x)
end

#%% Plotting
figure(figsize=(4, 3))
plot(x, y)
plot(x, x.*(x.^4 - 1)/20, linestyle="dashed")
xlabel(L"$x$")
ylabel(L"$y$")
legend(["Ritz solution", "Exact solution"])
tight_layout()
show()

Ambos tiene (casi) el mismo resultado y se muestra a continuación

Y si consideramos 3 términos en la expansion, obtenemos

Comparación Python/Julia

Respecto al número de líneas tenemos: 38 en Python y 38 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia.

Para Python:

%%timeit
mat, rhs = ritz(5, source)
c = solve(mat, -rhs)

con resultado

1000 loops, best of 3: 228 µs per loop

Para Julia:

function bench()
   mat, rhs = ritz(N, source)
   c = -mat\rhs
end
@benchmark bench()

con resultado

BenchmarkTools.Trial:
  memory estimate:  6.56 KiB
  allocs estimate:  340
  --------------
  minimum time:     13.527 μs (0.00% GC)
  median time:      15.927 μs (0.00% GC)
  mean time:        17.133 μs (4.50% GC)
  maximum time:     2.807 ms (97.36% GC)
  --------------
  samples:          10000
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 14 veces más lento que el de Julia.