Ir al contenido principal

Nicolás' blog

Reto de métodos numéricos: Día 27

Nicolás Guarín-Zapata

Comentarios

También disponible en:

English

Durante octubre (2017) estaré escribiendo un programa por día para algunos métodos numéricos famosos en Python y Julia. Esto está pensado como un ejercicio, no esperen que el código sea lo suficientemente bueno para usarse en la "vida real". Además, también debo mencionar que casi que no tengo experiencia con Julia, así que probablemente no escriba un Julia idiomático y se parezca más a Python.

Integración Monte Carlo

Hoy tenemos la integración Monte Carlo. En donde usamos muestreo aleatorio para calcular una integral numéricamente. Este método es importante cuando tenemos que evaluar integrales multidimensionales ya que las técnicas de cuadratura usuales implican un crecimiento exponencial con el número de puntos de muestreo.

El método cálcula una integral

\begin{equation*} I = \int_\Omega f(x) dx \end{equation*}

donde \(\Omega\) tiene volumen \(V\).

La integral es aproximada como

\begin{equation*} I \approx \frac{V}{N} \sum_{i=1}^{N} f(x_i) \end{equation*}

donde \(x_i\) está distribuido de manera uniforme sobre \(\Omega\).

A continuación se presenta el código.

Python

from __future__ import division, print_function
import numpy as np


def monte_carlo_int(fun, N, low, high, args=()):
    ndims = len(low)
    pts = np.random.uniform(low=low, high=high, size=(N, ndims))
    V = np.prod(np.asarray(high) - np.asarray(low))
    return V*np.sum(fun(pts, *args))/N


def circ(x, rad):
    return 0.5*(1 - np.sign(x[:, 0]**2 + x[:, 1]**2 - rad**2))


N = 1000000
low = [-1, -1]
high = [1, 1]
rad = 1
inte = monte_carlo_int(circ, N, low, high, args=(rad,))

Julia

using Distributions


function monte_carlo_int(fun, N, low, high; args=())
    ndims = length(low)
    pts = rand(Uniform(0, 1), N, ndims)
    for cont = 1:ndims
        pts[:, cont] = pts[:, cont]*(high[cont] - low[cont]) + low[cont]
    end
    V = prod(high - low)
    return V*sum(fun(pts, args...))/N
end


function circ(x, rad)
    return 0.5*(1 - sign.(x[:, 1].^2 + x[:, 2].^2 - rad^2))
end


N = 1000000
low = [-1, -1]
high = [1, 1]
rad = 1
inte = monte_carlo_int(circ, N, low, high, args=(rad,))

Una de los ejemplos más comunes es el cálculo de \(\pi\), esto se ilustra en la siguiente animación.

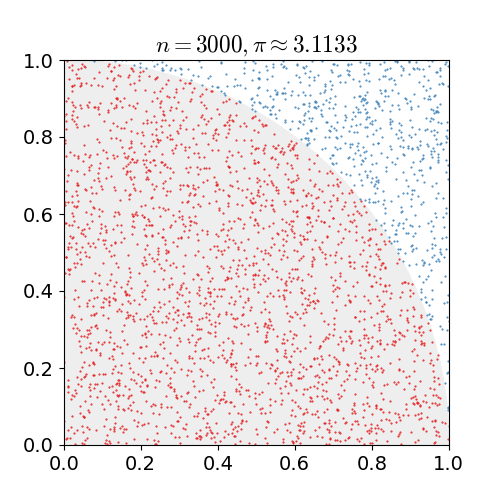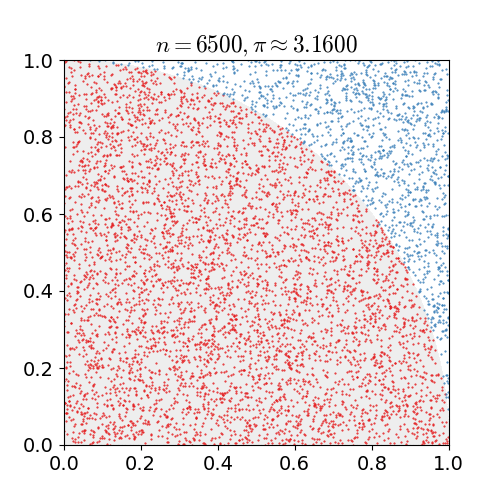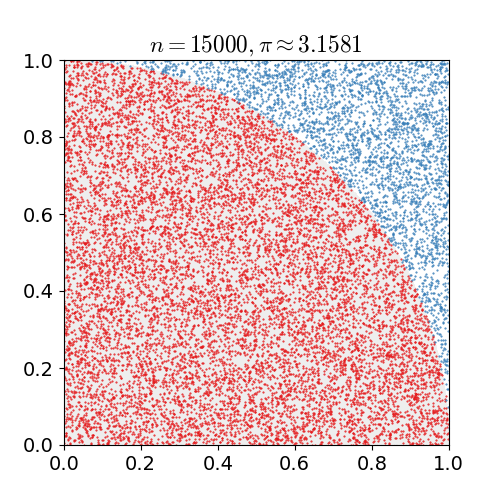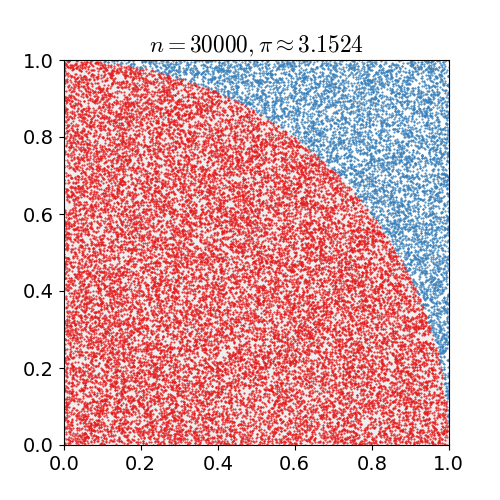
Aproximación de pi usando Monte Carlo.

Comparación Python/Julia

Respecto al número de líneas tenemos: 20 en Python y 24 en Julia. La comparación en tiempo de ejecución se realizó con el comando mágico de IPython %timeit y con @benchmark en Julia.

Para Python:

%timeit monte_carlo_int(circ, N, low, high, args=(rad,))

con resultado

10 loops, best of 3: 53.2 ms per loop

Para Julia:

@benchmark monte_carlo_int(circ, N, low, high, args=(rad,))

con result

BenchmarkTools.Trial:
  memory estimate:  129.70 MiB
  allocs estimate:  46
  --------------
  minimum time:     60.131 ms (5.15% GC)
  median time:      164.018 ms (55.64% GC)
  mean time:        204.366 ms (49.50% GC)
  maximum time:     357.749 ms (64.04% GC)
  --------------
  samples:          25
  evals/sample:     1

En este caso, podemos decir que el código de Python es alrededor de 3 veces más rápido que el de Julia.

Comentarios

Comments powered by Disqus