Skip to main content

Nicolás' blog

Numerical methods challenge: Day 2

Nicolás Guarín-Zapata

Comments

During October (2017) I will write a program per day for some well-known numerical methods in both Python and Julia. It is intended to be an exercise then don't expect the code to be good enough for real use. Also, I should mention that I have almost no experience with Julia, so it probably won't be idiomatic Julia but more Python-like Julia.

Regula falsi

The second method to be considered is the false position method, or regula falsi. This method is used to solve the equation \(f(x) = 0\) for \(x\) real, and \(f\) continuous. It starts with an interval \([a,b]\), where \(f(a)\) and \(f(b)\) should have opposite signs. The method is similar to bisection method but instead of halving the original interval it takes as a new point of the interval the intercept of the line that connect the function evaluated at the two extreme points. Then, the new point is computed from

\begin{equation*} c = \frac{a f(b) - b f(a)}{f(b) - f(a)} \end{equation*}

As in bisection method, we keep the interval where the solution appears, i.e., the sign of the function changes.

We will use the function \(f(x) = \cos(x) - x\) to test the codes, and the initial interval is \([0.5, \pi/4]\).

Following are the codes.

Python

from __future__ import division, print_function
from numpy import abs, cos, pi

def regula_falsi(fun, a, b, niter=50, ftol=1e-12, verbose=False):
    if fun(a) * fun(b) > 0:
        c = None
        msg = "The function should have a sign change in the interval."
    else:
        for cont in range(niter):
            qa = fun(a)
            qb = fun(b)
            c = (a*qb - b*qa)/(qb - qa)
            qc = fun(c)
            if verbose:
                print("n: {}, c: {}".format(cont, c))
            msg = "Maximum number of iterations reached."
            if abs(qc) < ftol:
                msg = "Root found with desired accuracy."
                break
            elif qa * qc < 0:
                b = c
            elif qb * qc < 0:
                a = c
    return c, msg

def fun(x):
    return cos(x) - x

print(regula_falsi(fun, 0.5, 0.25*pi))

Julia

function regula_falsi(fun, a, b, niter=50, ftol=1e-12, verbose=false)
    if fun(a) * fun(b) > 0
        c = nothing
        msg = "The function should have a sign change in the interval."
    else
        for cont = 1:niter
            qa = fun(a)
            qb = fun(b)
            c = (a*qb - b*qa)/(qb - qa)
            qc = fun(c)
            if verbose
                println("n: $(cont), c: $(c)")
            end
            if abs(fun(c)) < ftol
                msg = "Root found with desired accuracy."
                break
            elseif qa * qc < 0
                b = c
            elseif qb * qc < 0
                a = c
            end
            msg = "Maximum number of iterations reached."
        end
    end
    return c, msg
end

function fun(x)
    return cos(x) - x
end

println(regula_falsi(fun, 0.5, 0.25*pi))

Comparison

Regarding number of lines we have: 29 in Python and 32 in Julia. The comparison in execution time is done with %timeit magic command in IPython and @benchmark in Julia.

For Python:

%timeit regula_falsi(fun, 0.5, 0.25*pi)

with result

10000 loops, best of 3: 35.1 µs per loop

For Julia:

@benchmark regula_falsi(fun, 0.5, 0.25*pi)

with result

BenchmarkTools.Trial:
  memory estimate:  48 bytes
  allocs estimate:  2
  --------------
  minimum time:     449.495 ns (0.00% GC)
  median time:      464.371 ns (0.00% GC)
  mean time:        493.785 ns (0.52% GC)
  maximum time:     9.723 μs (92.54% GC)
  --------------
  samples:          10000
  evals/sample:     198

Numerical methods challenge

Nicolás Guarín-Zapata

Comments

For the next month I will write a program per day for some well-known numerical methods in both Python and Julia. It is intended to be an exercise, then don't expect the code to be good enough for real use. Also, I should mention that I have almost no experience with Julia, so it probably won't be idiomatic Julia but more Python-like Julia.

Day 1: Bisection method

The first method to be considered is the bisection method. This method is used to solve the equation \(f(x) = 0\) for \(x\) real, and \(f\) continuous. It starts with an interval \([a,b]\), where \(f(a)\) and \(f(b)\) should have opposite signs. The method then proceeds by halving the interval and selecting the one where the solution appears, i.e., the sign of the function changes.

We will use the function \(f(x) = \cos(x) - x^2\) to test the codes, and the initial interval is [0, 1].

The following are the codes:

Python

from __future__ import division, print_function
from numpy import log2, ceil, abs, cos

def bisection(fun, a, b, xtol=1e-6, ftol=1e-12):
    if fun(a) * fun(b) > 0:
        c = None
        msg = "The function should have a sign change in the interval."
    else:
        nmax = int(ceil(log2((b - a)/xtol)))
        for cont in range(nmax):
            c = 0.5*(a + b)
            if abs(fun(c)) < ftol:
                msg = "Root found with desired accuracy."
                break
            elif fun(a) * fun(c) < 0:
                b = c
            elif fun(b) * fun(c) < 0:
                a = c
            msg = "Maximum number of iterations reached."
    return c, msg

def fun(x):
    return cos(x) - x**2

print(bisection(fun, 0.0, 1.0))

With result

(0.824131965637207, 'Maximum number of iterations reached.')

Julia

function bisection(fun, a, b, xtol=1e-6, ftol=1e-12)
    if fun(a) * fun(b) > 0
        c = nothing
        msg = "The function should have a sign change in the interval."
    else
        nmax = ceil(log2((b - a)/xtol))
        for cont = 1:nmax
            c = 0.5*(a + b)
            if abs(fun(c)) < ftol
                msg = "Root found with desired accuracy."
                break
            elseif fun(a) * fun(c) < 0
                b = c
            elseif fun(b) * fun(c) < 0
                a = c
            end
            msg = "Maximum number of iterations reached."
        end
    end
    return c, msg
end

function fun(x)
    return cos(x) - x^2
end

println(bisection(fun, 0.0, 1.0))

With result

(0.824131965637207, "Maximum number of iterations reached.")

In this case, both codes are really close to each other. The Python code has 25 lines, while the Julia one has 27. As expected, the results given by them are the same.

Edit (2017-10-02)

As suggested by Edward Villegas, I decided to compare execution times. I used %timeit for IPython and @benchmark (from BenchmarkTools) for Julia.

In IPython, we have

%timeit bisection(fun, 0.0, 2.0)

with result

10000 loops, best of 3: 107 µs per loop

And in Julia, we have

@benchmark bisection(fun, 0.0, 2.0)

with result

BenchmarkTools.Trial:
  memory estimate:  48 bytes
  allocs estimate:  2
  --------------
  minimum time:     1.505 μs (0.00% GC)
  median time:      1.548 μs (0.00% GC)
  mean time:        1.604 μs (0.00% GC)
  maximum time:     38.425 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     10

And it seems that the Julia version is around 100 times faster than the Python counterpart.

Solution of the Schrödinger equation using Ritz method

Nicolás Guarín-Zapata

Comments

In this post, we describe the solution of the Schrödinger equation using the Ritz method and Hermite functions basis. This basis seems to be a good choice for the 1D Schrödinger equation since its an orthogonal basis over \((-\infty, \infty)\).

Transforming the equation to an algebraic one

We want so solve the time-independent Schrödinger equation

\begin{equation*} \left[-\frac{1}{2}\nabla^2 + V(x)\right] \psi = E\psi\, , \end{equation*}

where we are using natural units since they are a good choice for numeric calculations.

Solving this equation is equivalent to solve the following variational equation

\begin{equation*} \delta \Pi[\psi] = 0\, , \end{equation*}

with

\begin{equation*} \Pi[\psi] = \frac{1}{2} \langle \nabla \psi, \nabla\psi\rangle + \langle \psi, V(x) \psi\rangle - E\langle \psi, \psi\rangle \, , \end{equation*}

being \(\psi\) the wave function, \(V(x)\) the potential and \(E\) the energy. This variational formulation is equivalent to the time-independent Schrödinger equation, and \(E\) works as a Lagrange multiplier to enforce that the probability over the whole domain is 1.

We can expand the wave function in an orthonormal basis, namely

\begin{equation*} \psi = \sum_{n=0}^N c_n u_n(x)\, , \end{equation*}

where \(u_n(x) \equiv \mu_n H_n(x) e^{-x^2/2}\) is a normalized Hermite function, \(\mu_n\) is the inverse of magnitude of the \(n\)-th Hermite polynomial

\begin{equation*} \mu_n = \frac{1}{\sqrt{\pi^{1/2} n! 2^n}}\, , \end{equation*}

and \(c_n\) are the coefficients of the expansion. This representation is exact in the limit \(N \rightarrow \infty\).

If we replace the expansion in the functional, we obtain

\begin{equation*} \Pi_N = \sum_{m=0}^N\sum_{n=0}^N c_m c_n\left[ \frac{1}{2} \langle \nabla u_m, \nabla u_n\rangle + \langle u_m, V(x) u_n\rangle - E^N \delta_{mn}\right]\, . \end{equation*}

The integrand of the integral involving the two derivatives reads

\begin{align*} u_m' u_n' =& \left[2m \frac{\mu_{m-1}}{\mu_m}u_{m-1} - x u_m\right] \left[2n \frac{\mu_{n-1}}{\mu_n}u_{n-1} - x u_n\right]\\ =& 4mn\frac{\mu_{m-1} \mu_{n-1}}{\mu_m \mu_n} u_{n-1} u_{m-1} - 2m\frac{\mu_{m-1}}{\mu_{m}}x u_{m-1} u_n\\ &- 2n\frac{\mu_{n-1}}{\mu_{n}}x u_{n-1} u_m + x^2 u_m u_n \end{align*}

Thus, the kinetic energy term reads

\begin{align*} \langle \nabla u_m, \nabla u_n \rangle =& 4mn\frac{\mu_{m-1} \mu_{n-1}}{\mu_m \mu_n} \langle u_{n-1}, u_{m-1}\rangle - 2m\frac{\mu_{m-1}}{\mu_{m}} \langle u_{m-1}, x u_n\rangle\\ &- 2n\frac{\mu_{n-1}}{\mu_{n}} \langle u_{m}, x u_{n - 1}\rangle + \langle u_m, x^2 u_n\rangle\\ =& 4mn \frac{\mu_{m-1}^2}{\mu_m^2}\delta_{mn} - 2m \frac{\mu_{m-1}}{\mu_m} \alpha_{m-1, n} - 2n \frac{\mu_{n-1}}{\mu_n} \alpha_{m, n-1} + \beta_{mn} \, , \end{align*}

with

\begin{equation*} \alpha_{m,n} \equiv \langle u_{m}, x u_n\rangle = \begin{cases} \sqrt{\frac{n + 1}{2}} & m=n +1\\ \sqrt{\frac{n}{2}} & m=n - 1\\ 0 & \text{otherwise}\end{cases}\, , \end{equation*}

and

\begin{equation*} \beta_{m,n} \equiv \langle u_{m}, x^2 u_n\rangle = \begin{cases} \frac{\sqrt{n(n-1)}}{2} & m = n - 2\\ \frac{2n + 1}{2} & m = n \\ \frac{\sqrt{(n+1)(n+1)}}{2} & m = n + 2 \\ 0 & \text{otherwise}\end{cases}\, . \end{equation*}

The functional is rewritten as

\begin{align*} \Pi_N =& \sum_{m=0}^N \sum_{n=0}^N c_m c_n \left[2mn \frac{\mu^2_{m-1}}{\mu^2_m}\delta_{mn} - m\frac{\mu_{m-1}}{\mu_m}\alpha_{m - 1, n} - n\frac{\mu_{n-1}}{\mu_n}\delta_{m, n-1} \right.\nonumber \\ &\left. - \frac{1}{2}\beta_{mn} + \langle u_m, V(x) u_n\rangle - E^N \delta_{mn}\right] \, . \end{align*}

Taking the variation

\begin{equation*} \delta \Pi_N = 0\, , \end{equation*}

that in this case is equivalent to

\begin{equation*} \frac{\partial \Pi_N}{\partial c_i} = 0\quad \forall i=0, 1, \cdots N\, , \end{equation*}

yields to

\begin{equation*} [H]\lbrace c\rbrace = E^N\lbrace c\rbrace \, , \end{equation*}

where the components of the matrix \([H]\) are given by

\begin{equation*} H_{mn} = 2mn \frac{\mu^2_{m-1}}{\mu^2_m}\delta_{mn} - m\frac{\mu_{m-1}}{\mu_m}\alpha_{m - 1, n} - n\frac{\mu_{n-1}}{\mu_n}\delta_{m, n-1} - \frac{1}{2}\beta_{mn} + \langle u_m, V(x) u_n\rangle\, . \end{equation*}

The last integral can be computed using Gauss-Hermite quadrature. And we will need more Gauss points if we want to integrate higher-order polynomials. This method would work fine for functions that can be approximated by polynomials.

Examples

A Python implementation of this method is presented in this repo.

For all the examples we use the following imports

from __future__ import division, print_function
import numpy as np
from hermite_QM import *

Quantum harmonic oscilator

In this case the (normalized) potential is given by

\begin{equation*} V(x) = \frac{1}{2} x^2 \end{equation*}

and the exact normalized eigenvalues are given by

\begin{equation*} E_n = n + \frac{1}{2} \end{equation*}

The following snippet computes the first 10 eigenvalues and plot the corresponding eigenstates

potential = lambda x: 0.5*x**2
vals, vecs = eigenstates(potential, nterms=11, ngpts=12)
print(np.round(vals[:10], 6))
fig, ax = plt.subplots(1, 1)
plot_eigenstates(vals, vecs, potential);

with results

[ 0.5  1.5  2.5  3.5  4.5  5.5  6.5  7.5  8.5  9.5]
/images/hermite_ritz_harmonic.svg

Absolute value potential

potential = lambda x: np.abs(x)
vals, vecs = eigenstates(potential)
print(np.round(vals[:10], 6))
fig, ax = plt.subplots(1, 1)
plot_eigenstates(vals, vecs, potential, lims=(-8, 8));

with results

[ 0.811203  1.855725  2.57894   3.244576  3.826353  4.38189   4.895365
  5.396614  5.911591  6.421015]
/images/hermite_ritz_abs.svg

Cubic potential

potential = lambda x: np.abs(x/3)**3
vals, vecs = eigenstates(potential)
print(np.round(vals[:10], 6))
fig, ax = plt.subplots(1, 1)
plot_eigenstates(vals, vecs, potential, lims=(-6, 6));

with results

[ 0.180588  0.609153  1.124594  1.681002  2.272087  2.889805  3.530901
  4.191962  4.871133  5.566413]
/images/hermite_ritz_cubic.svg

Harmonic with quartic perturbation

potential = lambda x: 0.5*x**2 + 0.1*x**4
vals, vecs = eigenstates(potential, nterms=20, ngpts=22)
print(np.round(vals[:10], 6))
fig, ax = plt.subplots(1, 1)
plot_eigenstates(vals, vecs, potential, lims=(-5, 5))

with results

[  0.559146   1.769503   3.138624   4.628884   6.220303   7.899789
   9.658703  11.489094  13.38638   15.361055]
/images/hermite_ritz_pert_harm.svg

A Jupyter Notebook with the examples can be found here.

Using style sheets with matplotlib

Nicolás Guarín-Zapata

Comments

We can format plots easily using the style package in matplotlib all. The main idea is to create a file with some of the parameters that want to be defined (that can also be accessed through rcParams).

This post is not a tutorial on how to use those, for that you can check the style sheet reference. Here, I just want to play with some of these parameters to create three different styles. The first two examples present the style of an (infamous by some) software, that is probably used for most people as their visualization platform, while the third one is just a clean style. All the files used here can be download here.

For all the examples below the following imports are done:

from __future__ import division, print_function
import numpy as np
import matplotlib.pyplot as plt

First example: MS 2003

In our first example we want to reproduce the style that we used to see more than a decade ago as default.

The following is the content of the file MS2003.mplstyle

font.family : sans-serif

axes.facecolor : c0c0c0
axes.edgecolor : black
axes.prop_cycle : cycler('color',['000080', 'FF00FF', 'FFFF00', '00FFFF','800080', '800000', '008080', '0000FF'])
axes.grid : True

axes.spines.left   : True
axes.spines.bottom : True
axes.spines.top    : True
axes.spines.right  : True

grid.color : black
grid.linestyle : -

lines.linewidth : 1

figure.figsize : 5, 3

legend.fancybox : False
legend.frameon : True
legend.facecolor : white
legend.edgecolor : black
legend.loc : center left

The following code use this style

style = "MS2003.mplstyle"
with plt.style.context(style):
    x = np.linspace(0, 4, 100)
    y = np.sin(np.pi*x + 1e-6)/(np.pi*x + 1e-6)
    fig = plt.figure()
    ax = plt.subplot(111)
    for cont in range(5):
        plt.plot(x, y/(cont + 1), label=cont)

    plt.gca().xaxis.grid(False)
    box = ax.get_position()
    ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
    plt.legend(bbox_to_anchor=(1, 0.5))

and this is the result

/images/MS2003_style.svg

Second example: MS 2007

In the second example we want to reproduce the offspring of the style in the first example. This is definitely an improvement over the previous style, but it is not perfect.

The following is the content of the file MS2007.mplstyle

font.family : sans-serif

axes.facecolor : white
axes.edgecolor : 4d4d4d
axes.prop_cycle : cycler('color',['4573a7', 'aa4644', '89a54e', '71588f','4298af', 'db843d', '93a9d0', 'd09392'])
axes.grid : True
axes.linewidth : 0.5

axes.spines.left   : True
axes.spines.bottom : True
axes.spines.top    : False
axes.spines.right  : False

lines.linewidth : 2

grid.color : 4d4d4d
grid.linestyle : -
grid.linewidth : 0.5

figure.figsize : 5, 3

legend.fancybox : False
legend.frameon : False
legend.facecolor : white
legend.edgecolor : 4d4d4d
legend.loc : center left

The following code use this style

style = "MS2007.mplstyle"
with plt.style.context(style):
    x = np.linspace(0, 4, 100)
    y = np.sin(np.pi*x + 1e-6)/(np.pi*x + 1e-6)
    fig = plt.figure()
    ax = plt.subplot(111)
    for cont in range(5):
        plt.plot(x, y/(cont + 1), label=cont)

    plt.gca().xaxis.grid(False)
    box = ax.get_position()
    ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
    plt.legend(bbox_to_anchor=(1, 0.5))

and this is the result

/images/MS2007_style.svg

Third example: a clean style

The last example is a clean style that uses a color palette taken from ColorBrewer.

The following is the content of the file clean_style.mplstyle

font.family : sans-serif

axes.facecolor : white
axes.prop_cycle : cycler('color',['e41a1c', '377eb8', '4daf4a', '984ea3', 'ff7f00', 'ffff33', 'a65628', 'f781bf'])
axes.linewidth : 0.0
axes.grid : True

lines.linewidth : 1.5

xtick.direction : in
ytick.direction : in

grid.color : c7dedf
grid.linestyle : -
grid.linewidth : 0.3

figure.figsize : 6, 4

legend.fancybox : False
legend.frameon : False
legend.loc : best

The following code use this style

style = "clean.mplstyle"
with plt.style.context(style):
    x = np.linspace(0, 4, 100)
    y = np.sin(np.pi*x + 1e-6)/(np.pi*x + 1e-6)
    fig = plt.figure()
    ax = plt.subplot(111)
    for cont in range(5):
        plt.plot(x, y/(cont + 1), label=cont)

    plt.legend()

and this is the result

/images/clean_style.svg

We can also use files that are stored remotely. For example, in the third example we could have used the following URL:

style = "https://raw.githubusercontent.com/nicoguaro/matplotlib_styles/master/styles/clean.mplstyle"

Resources

As I mentioned above, the objective of this post was jut to create some simple-enough style-sheets for matplotlib and see them in action.

This post does not pretend to be a guide for good plots/visualization. For that matter you better look for some references, for example:

Also, I found really useful the following tools:

  • ColorBrewer2 allows to pick colormaps with different criteria (quantitative/qualitative, printer friendly, colorblind friendly).

  • ColRD has plenty of color palettes. It also has the option to generate palettes from images.

  • Colorgorical is a tool to make categorical color palettes for information visualization.

Piecewise Hermite interpolation

Nicolás Guarín-Zapata

Comments

In this post, we find the Hermite interpolation functions for the domain [-1, 1]. And then, we use it for a pieciwise interpolation. Notice that this interpolation has \(C^1\) continuity compared to the \(C^0\) continuity that is common in Lagrange interpolation.

To compute the polynomials explicitly we use sympy.

from __future__ import division
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

We want to find a set of basis function that satisfy the following

\begin{align*} N_1(x_1) &= 1\\ N_1(x_2) &= 0\\ N_2(x_1) &= 1\\ N_2(x_2) &= 0\\ N'_3(x_1) &= 1\\ N'_3(x_2) &= 0\\ N'_4(x_1) &= 1\\ N'_4(x_2) &= 0 \end{align*}

These can be written as

\begin{equation*} \begin{bmatrix} 1 &x_1 &x_1^2 &x_1^3\\ 1 &x_2 &x_2^2 &x_2^3\\ 0 &1 &2x_1 &3x_1^2\\ 0 &1 &2x_2 &3x_2^2 \end{bmatrix} \begin{bmatrix} a_{11} &a_{12} &a_{13} &a_{14}\\ a_{21} &a_{22} &a_{23} &a_{24}\\ a_{31} &a_{32} &a_{33} &a_{34}\\ a_{41} &a_{42} &a_{43} &a_{44} \end{bmatrix} = \begin{bmatrix} 1 &0 &0 &0\\ 0 &1 &0 &0\\ 0 &0 &1 &0\\ 0 &0 &0 &1 \end{bmatrix} \end{equation*}

The formula for interpolation would be

\begin{equation*} f(x) \approx N_1(x) u_1 + N_2(x) u_2 + |J|(N_3(x) u'_3 + N_4(x) u'_4)\quad \forall x\in [a, b] \end{equation*}

with \(|J| = (b - a)/2\) the Jacobian determinant of the transformation.

x1, x2, x = sym.symbols("x1 x2 x")
V = sym.Matrix([
    [1, x1, x1**2, x1**3],
    [1, x2, x2**2, x2**3],
    [0, 1, 2*x1, 3*x1**2],
    [0, 1, 2*x2, 3*x2**2]])
V
\begin{equation*} \left[\begin{matrix}1 & x_{1} & x_{1}^{2} & x_{1}^{3}\\ 1 & x_{2} & x_{2}^{2} & x_{2}^{3}\\ 0 & 1 & 2 x_{1} & 3 x_{1}^{2}\\ 0 & 1 & 2 x_{2} & 3 x_{2}^{2}\end{matrix}\right] \end{equation*}

We can see that the previous matrix is a confluent Vandermonder matrix [1]. It is similar to a Vandermonde matrix for the first \(n\) nodes and the derivatives of each row for the following ones.

The coefficients for our polynomials are given by the inverse of this matrix.

sym.simplify(V.inv())
\begin{equation*} \left[\begin{matrix}\frac{x_{2}^{2} \left(3 x_{1} - x_{2}\right)}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & \frac{x_{1}^{2} \left(x_{1} - 3 x_{2}\right)}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & - \frac{x_{1} x_{2}^{2}}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}} & - \frac{x_{1}^{2} x_{2}}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}}\\- \frac{6 x_{1} x_{2}}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & \frac{6 x_{1} x_{2}}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & \frac{x_{2} \left(2 x_{1} + x_{2}\right)}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}} & \frac{x_{1} \left(x_{1} + 2 x_{2}\right)}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}}\\\frac{3 x_{1} + 3 x_{2}}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & - \frac{3 x_{1} + 3 x_{2}}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & - \frac{x_{1} + 2 x_{2}}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}} & - \frac{2 x_{1} + x_{2}}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}}\\- \frac{2}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & \frac{2}{x_{1}^{3} - 3 x_{1}^{2} x_{2} + 3 x_{1} x_{2}^{2} - x_{2}^{3}} & \frac{1}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}} & \frac{1}{x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}}\end{matrix}\right] \end{equation*}

And we replace the values for the extreme nodes, -1 and 1.

V_inv = sym.simplify(V.subs({x1:-1, x2:1}).inv())
V_inv
\begin{equation*} \left[\begin{matrix}\frac{1}{2} & \frac{1}{2} & \frac{1}{4} & - \frac{1}{4}\\ - \frac{3}{4} & \frac{3}{4} & - \frac{1}{4} & - \frac{1}{4}\\ 0 & 0 & - \frac{1}{4} & \frac{1}{4}\\ \frac{1}{4} & - \frac{1}{4} & \frac{1}{4} & \frac{1}{4}\end{matrix}\right] \end{equation*}

The polynomials are the product of the coefficients and the monomials

sym.factor(V_inv.T * sym.Matrix([1, x, x**2, x**3]))
\begin{equation*} \left[\begin{matrix}\frac{1}{4} \left(x - 1\right)^{2} \left(x + 2\right)\\- \frac{1}{4} \left(x - 2\right) \left(x + 1\right)^{2}\\\frac{1}{4} \left(x - 1\right)^{2} \left(x + 1\right)\\\frac{1}{4} \left(x - 1\right) \left(x + 1\right)^{2}\end{matrix}\right] \end{equation*}

The interpolation basis would be

\begin{align*} N_1 (x) &= \frac{1}{4} (x - 1)^2 (2 + x)\\ N_2 (x) &= \frac{1}{4} (x + 1)^2 (2 - x)\\ N_3 (x) &= \frac{1}{4} (x - 1)^2 (x + 1)\\ N_4 (x) &= \frac{1}{4} (x + 1)^2 (x - 1)\, , \end{align*}

and the following function computes the interpolation for a given function and derivative

def hermite_interp(fun, grad, x0=-1, x1=1, npts=101):
    jaco = (x1 - x0)/2
    x = np.linspace(-1, 1, npts)
    f1 = fun(x0)
    f2 = fun(x1)
    g1 = grad(x0)
    g2 = grad(x1)
    N1 = 1/4*(x - 1)**2 * (2 + x)
    N2 = 1/4*(x + 1)**2 * (2 - x)
    N3 = 1/4*(x - 1)**2 * (x + 1)
    N4 = 1/4*(x + 1)**2 * (x - 1)
    interp = N1*f1 + N2*f2 + jaco*(N3*g1 + N4*g2)
    return interp

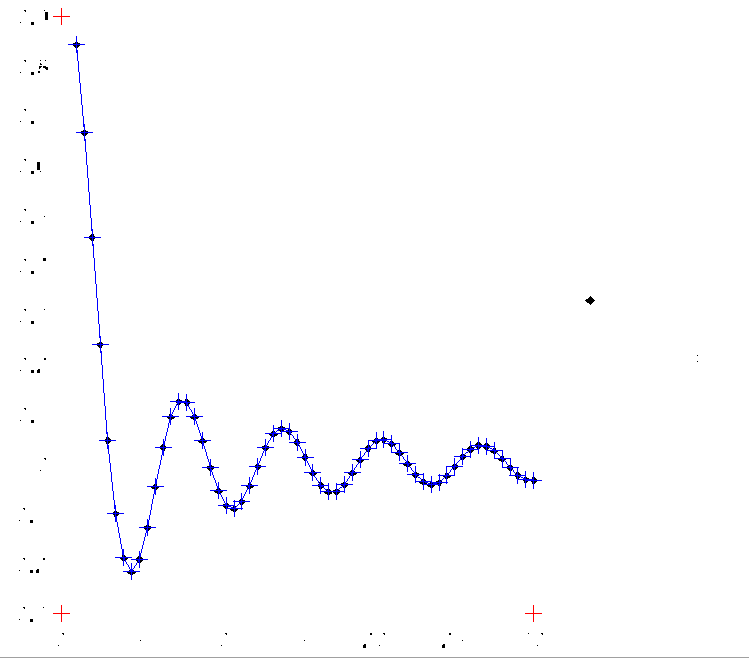
In this case, we interpolate the sinc function

def fun(x):
    return np.sin(2*np.pi*x)/(2*np.pi*x)


def grad(x):
    return np.cos(2*np.pi*x)/x - np.sin(2*np.pi*x)/(2*np.pi*x**2)

The following snippet compute the interpolation and plot it.

a = 2
b = 5
nels = 7
npts = 200
x = np.linspace(a, b, npts)
y = fun(x)
plt.plot(x, y, color="black")
xi = np.linspace(a, b, num=nels, endpoint=False)
dx = xi[1] - xi[0]
for x0 in xi:
    x1 = x0 + dx
    x = np.linspace(x0, x1, npts)
    y = hermite_interp(fun, grad, x0=x0, x1=x1, npts=npts)
plt.plot(x, y, linestyle="dashed", color="#4daf4a")
plt.plot([x[0], x[-1]], [y[0], y[-1]], marker="o", color="#4daf4a",
         linewidth=0)
plt.xlabel("x")
plt.ylabel("y")
plt.legend(["Exact function", "Interpolation"])
plt.show()
/images/sinc_interp.svg

References

(Auxiliary) Tools for research

Nicolás Guarín-Zapata

Comments

In this post I want to talk about some tools (or something like that) that are useful in the day-to-day research, but usually not so popular for being somewhat tangential to the area specific in which each one works.

Scripting

A script is a usually simple program that performs a series of tasks. If there is a task that must be done more than ... five times (the number varies according to the patience), then I think it's something we can ask the computer to do for us. In other words: we can automate that work. Some tasks that can be a good alternative to automate are: rename 100 files, convert a file from one format to another (e.g. STL to OBJ), read 387 files with information on the climate and graph its evolution temporary (minimum, maximum and average temperature). These tasks can be easy to do by hand, but for the amount of work that they involve are tedious.

The first thing to do is to get a scripting language. Some options are Python, Bash, Julia, Matlab/Octave, Scilab. Allowing myself to follow my bias, I would recommend to use Python.

Graphics and schematics

A picture is worth a thousand words, or so the saying goes. Personally, it seems absolutely true to me and I try to do scribbles to better understand something or explain it better. The first thing I would like to mention is the difference between images bitmap (or raster) and vector images.

  • Bitmap image: it's an image which is represented by an array (or rectangular grid) of pixels. In other words, the color information that there are in each point of the image. The most popular formats store the compressed information. For high contrast graphics (such as schematics or diagrams) the best format is PNG. If you have an animation, GIF would be preferable. And in the case of photographs it is better to use JPG.

  • Vector image: is an image that is made up of geometric entities. In this case, the stored information is not point-to-point but the construction of the shapes that constitute it. For this reason, these images don't pixelate because the information you have is how to build it. This type of images is the best options for schematics and diagrams, since the only stored information are the strokes and text added to them (see Figure 1). The de facto standard for this type of images is PDF —it is the one I usually include in my documents \(\LaTeX\), although there is a way to embed SVG in \(\LaTeX\) But it's something I haven't yet explored. Although PDF is the standard, the preferred format is SVG (Scalable Vector Graphics) which is a standard across the internet and most modern browsers allow viewing.

Recapping, we should use JPG images for photographs and SVG for schematics/diagrams. Another attribute that may be useful is the Layer management, SVG allows this ... and for raster formats we have the option to use TIFF.

Regarding software to generate/edit this type of images I must say that there are a large number of programs that allow exporting to these formats: Python/Matplotlib, Matlab, Inkscape, Adobe Illustrator, GIMP, Photoshop, LibreOffice. If the graph is generated from a calculation or a data series I use Matplotlib. If instead, we want to make a schematic or my tool of choice is Inkscape. This program is intended to be a free alternative to programs like Adobe Illustrator —and it does achieve it. Obviously, you could use Illustrator or Corel Draw for this task. If the only use would be to make Technical schematics, I think it would be a waste.

/images/sensor_hall.png

Figure 1. Schematic for magnetic field sensing for permanent magnets using Hall effect. From my Engineering Physics thesis .

Taking notes

I suppose that to some it would seem a bit trivial to speak of "notetaking" and much more coming from someone who didn't have notebooks in high school, but since I'm a bit stubborn I think I'll still write a little about this. The first thing I would like to mention is that I remember people talking to me about this at school, but there was never anything formal regarding developing these skills. Surfing the web, there is a lot of information. Even the Wikipedia article on English is interesting. There is nothing better to write than to have a good pen and paper with a good grammage, that's why I still use a notebook where I keep track of what I do in my research and take notes. However, this scheme is quite linear and leaves out more contemporary options. That is, why settle for a document in this time of hyper-documents? The advantages of taking notes digitally jump to the eye, in a hyper-document you can have links, embed images, video and sound.

Regarding tools, I include a short list here:

  • Evernote is probably the most popular tool for taking notes. It's cross-platform, Freemium (free basic and paid advanced functionality), and has many options. I use it, but not much in my research.

  • Zim it is an offline wiki. Has great number of options like calendar, equations with \(\LaTeX\), images ... anyway. The but that I find is that no I have managed to configure the equations in Windows (and in my office I must use Windows :-/).

  • Docear this is a tool thought, mainly, to handle bibliography. However, it allows to take notes and, in general, handle the information of the investigation. The more (or less) appealing feature is that it works around mental maps.

  • Zotero It is also a tool to handle bibliography, although it allows to handle some note taking (at least around the bibliography).

  • Mendeley it is very similar to the previous one, although with more functionalities. The biggest but that I find it is that in 2013 it was bought by Elsevier.

Regarding bibliography management I would also like to mention EndNote which is the program with the longest trajectory and JabRef which is the one that I have used the longest. Some interesting references comparing bibliography handlers are:: [A] [B] [C].

Graphic reconstruction

It is common to find information presented in the form of graphics. It is also common that we want to have the numerical data of these graphs to be able to compare them with ours. To know if our measurements/simulations/methods give results similar to others presented in the literature. We could use powerful image processing software, or other more modest ones designed specifically for this purpose.

/images/pointplot.jpg

Figure 2. Original graphic.
/images/digitized_pts.png

Figure 3. Graphic processed in Engauge Digitizer. Some points were selected (automatically) to obtain their coordinates.

  • Digitizer of XY chart this is a plugin for Libreoffice/OpenOffice and it exports the result to the current spreadsheet, it is simple and easy to use.

  • Engauge Digitizer, is the one I normally use when I need to do this task (see Figures above). It is open source (and free) and has a fair amount of options to make the task easier.

  • Plot Digitizer I don't have a lot of information about this one (since I have never used it), except that it is written in Java.

  • ImageJ this is a (complete) program for image processing that is written in Java. I have not used it for this task on a regular basis, but could be used for it.

Scientific visualization

Scientific visualization is in charge of generating graphs that allow visualizing "scientific data" to facilitate the understanding behind the data. For this work, many of us have used scripting languages such as Matlab/Octave, Scilab or Python (with Matplotlib or Mayavi). However, as visualization is about something visual —what else?—, it is good have a tool that allows you to generate and change graphics interactively, although we must always automate as much amount of work possible (laziness has always been one of the largest mobiles of humanity, you have to accept it).

  • MayaVi, this is a program written in Python that uses VTK. It is very versatile and the great advantage it has is that it can be used within Python scripts.

  • Paraview, this program is also based on VTK and allows to parallelize the work (for multi-core computers and clusters). Below I include a video generated in Paraview to show its capabilities.

  • Visit, this program is also VTK based, I have never used it but I wanted to include it because people say it can be more intuitive than Paraview.

  • Tecplot, this program is very popular at Purdue. I think it was initially intended for CFD, but it has been much expanded. Regarding 3D graphics, it does not seem better than ParaView, however, the 2D graphics capabilities (XY graphics, and others) make it attractive.

  • Scavis, this is written in Java. I didn't know it until I started writing this post but it caught my eye and I wante to put it on the list. Something that cught my attention is that it allows scripting in several languages: Java, Python, Ruby, BeanShell, and Matlab/Octave.

  • Origin, I have never used it but I didn't want to leave it out because I've always heard great things about it (probably comparing it with Excel ... but I can't comment).

Cross fire simulation Vimeo.

Version control

Version control is the management of changes in documents, source code and other types of information. This can be done manually, but it is easy to make mistakes or replace the version of a code easily, and for this it is advisable to use software that facilitates the work. The idea is to have a place (repository) where versions and changes are stored, and keep track of them. In this way you can revert to a previous version of documents and multiple people can work together. There are two paradigms (or architectures) for version control: centralized and distributed. In the first there is a centralized repository where you find all the information. In distributed architectures each user has a copy of the repository. Personally I have only used Git, which falls under the distributed category and is one of the most popular version contorl software at the moment; it is used by companies like Google, Facebook and Netflix.

An example can be seen in this repository, with the undergrad thesis document of Santiago Echeverri, which I had the opportunity to advise. We edited this document together while he was in Medellin and I was in USA. The document was made in the markup language \(\LaTeX\).

In addition to having control over the versions and being able to access previous versions, it is useful to be able to store the information in a accesible location from anywhere in the world with a connection to Internet. This can be achieved with your own server, obviously, or also through an external provider. Two projects that are very popular for hosting repositories are (comparison between Github and BitBucket):

  • Github is the most popular at the moment. It allows to have projects with an unlimited number of collaborators. To have a private repository it is necessary to pay.

  • BitBucket has the main advantage that allows you to have private repositories without the need to pay. It is only free for projects with 5 or fewer collaborators (or for academic projects).

La zorra y las uvas

Nicolás Guarín-Zapata

Comments

Mirando en internet no encontré una versión en español de la fábula de Esopo "La zorra y las uvas" que me gustara (o que al menos rimara :P). De hecho, el artículo de Wikipedia en español es bastante más malo que su equivalente en inglés.  Por esto, y por petición de una amiga, hice mi versión con rima asonante. Y reza así

La Zorra y las uvas

La zorra que con ansias uvas buscaba
no pudo alcanzarlas por lo alto que estaban.
Giró y exclamó, con risa lastimera:
¡Están verdes! No valen mi espera.

Note taking with my tablet

Nicolás Guarín-Zapata

Comments

Last year baby Jesus gave me a Samsung Galaxy Note 10.1 (model 2012). This tablet is designed for taking notes, as it brings an S-Pen (made by Wacom, which I think makes the technology for most commercial tablets) and various applications designed for it. Such as: S Note, PhotoShop Touch, Crayon Physics (you have to play it is very fun).

So I decided to make an experiment taking notes in class with my tablet completely in the two subjects I studied in the spring 2014 term. In Optimization I used the pencil that came with the tablet and for Molecular Physics I used a Bamboo Stylus which is supposed to be designed specifically for this tablet. I took notes with the default software (S Note) and converted to PDF (the notes were made entirely with the software):

Although the touch sensation of the Bamboo Stylus is much more pleasant, the performance of the S Pen is much better. In both cases, the feeling is very different from using paper and pencil (pen/fountain pen), largely because friction is very little in comparison (something that is better with conductive pencils). The user experience of the pencil varies greatly from one application to another, resulting in good expectations. As for taking notes: it is highly recommended to take short notes (like meetings); not so much for taking long notes (like class notes), unless you want to have a digital copy easily.

Apps

The technology behind the tablet is the most important part. Simply pu, the pen has an antenna and the tablet a grid of antennas that are tuned to the same frequency (531 kHz, in this link they explain how it works a little better). However, it is also important to consider the software that is used to take notes:

S Note

  • It is the native app for taking notes.

  • It has shape and equations recognition. Equations should be simple, don't expect to take notes of Quantum Mechanics or Continuum Mechanics using this tool.

  • It allow to insert images and record sound within the app.

  • It has "palm rejection".

  • The size of the page is not configurable.

Papyrus

  • It has "palm rejection" and allow to setup your finger as eraser (this can be very useful).

  • It allows different page sizes and backgrounds.

  • It allows to draw rectangles and ellipses.

  • Brushes are very basic.

Note Anytime

  • It allows to have different page sizes.

  • It stores paths as vector graphics and you cand edit them (change color size or style) later.

  • It has several brushes and they are even customizable.

  • It can't convert notes to PDF.

  • It does not have "palm rejection".

Quill

  • It is open source, although if you get it through "Google Store" it has a cost.

  • The algorithm for path recognition is better than the others (and it is adjustable).

  • It is still in a preliminary stage.

Sadly, there isn't a version of Paper (by FiftyThree) on Android, and, although there is a version of Bamboo Paper (by Wacom) for Android it is not compatible with the tablet.

In conclusion

Replacing "traditional" note taking with "digital" notes It may be a bit rushed, but it is doable. The application that comes by default (S Note) allows to do the job "out of the box", but it could be better. The applications that I find the most Promising are: Note Anytime and Quill.

Palabras terminadas en "ar", "er" o "ir"

Nicolás Guarín-Zapata

Comments

Cuando estaba en el colegio, en ocasiones mencionaban las palabras terminadas en "ar", "er" o "ir" —iguales al final de nuestros verbos en infinitivo— que no eran verbos. Eran pocos ejemplos los que mencionaban, así que algunos años después me dio el arrebato de hacer una lista… y hela aquí:

AR

AR

AR

ER

IR

agar

dispar

pajar

alfiler

cachemir

ajuar

ejemplar

paladar

alquiler

casimir

alar

escolar

palatar

amater

elixir

albañar

espectacular

palomar

anteayer

emir

albar

estelar

papilar

antier

faquir

alfar

extracurricular

par

atelier

kefir

alizar

familiar

paramilitar

ayer

menhir

almiar

fular

particular

bachiller

nadir

almimbar

globular

peculiar

bereber

porvenir

alminar

hangar

pendular

brigadier

sir

altar

hogar

peninsular

canciller

souvenir

alveolar

ijar

perpendicular

cualquier

visir

antealtar

impar

pilar

doquier

zafir

antisolar

insular

pinar

dossier

ar

intercelular

planar

enser

auricular

intraocular

polar

ester

avatar

jaguar

policelular

menester

axilar

juglar

pulgar

mercader

azahar

lagar

pulmonar

micer

azar

lanar

quasar

neceser

bacillar

lar

radar

palier

bar

limonar

radicular

placer

bazar

llar

rectangular

plumier

bicelular

lobular

reticular

premier

bienestar

lodazar

samovar

primer

bifilar

lugar

secular

rosicler

biliar

lunar

seglar

salmer

billar

malar

semicircular

somier

binocular

maleolar

semilunar

sumiller

bipolar

malvar

similar

taller

broncopulmonar

mandibular

solar

tercer

bulevar

manglar

subcelular

veguer

calamar

manillar

supraclavicular

calcañar

manjar

supralunar

capilar

mar

telar

capsular

maxilar

testicular

caviar

melocotonar

tisular

celular

melonar

trifilar

centenar

membrillar

trufar

ciliar

miliar

tubular

clavicular

militar

tular

collar

millar

ultramar

consular

molar

uvular

coplanar

mollar

vascular

crepuscular

muladar

vehicular

corpuscular

monocelular

vermicular

cuadrangular

mular

vesicular

cular

muscular

vulgar

curricular

nuclear

yugular

dactilar

ocular

zar

dinar

olivar

Si tienes alguna sugerencia de palabra que haga falta la puedes dejar en los comentarios.

Última actualización: Octubre 21, 2022.

Descargar la lista en formato CSV o en formato XLS.

About teleportation in Star Trek

Nicolás Guarín-Zapata

Comments

A friend once asked me about which of two methods was easier to teleport people. One consisted of "deconfiguring" and "reconfiguring" the person (as information, similar to Start Trek and the other in "creating a shortcut" between two places in space-time to pass to the person. Obviously, in both cases assuming that such things can be done.

Regarding the creation of the shortcut in space-time, I think I have not studied the equations of General Relativity to be able to do the math, although perhaps in Física Pasión give us these calculations.

The first of the alternatives consists of, basically, the representation of a person as information and its "deconfiguration" processing, transmission and processing of "reconfiguration". Since as humans we are made, mostly, of water we will assume a person of water for the calculations. We will also take as reference mass \(70\, \mbox {kg}\).

Some data that we will use are:

  • The molar mass of water is \(M_{H_2O}=18,01528\ \mbox{g/mol}\);

  • Avogradro number is \(N_A=6,022 \times 10^{23}/\mbox{mol}\).

Then, we have that the number of moles in a person is

\begin{equation*} m_\text{persona} = \frac{70\ \mbox{kg}\ \mbox{moles}} {18,015\times 10^{-3} \text{kg}} =3885,7\ \mbox{moles}\, , \end{equation*}

and the number of molecules is

\begin{equation*} N_\text{moleculas} = N_A m_\text{persona} = 2,34\times 10^{27}\ \mbox{moleculas}\, . \end{equation*}

Water has 12 vibrational and 6 translational modes, and furthermore 40 quantum electronic numbers. This add up to 58 degrees of freedom for each molecule. Thus, the total number of degrees of freedom is

\begin{equation*} N_{GDL} = 1,36\times 10^{29}\, . \end{equation*}

In 2011 there was a transmission record of 186 Gb/s, considering this rate the time it would take to transmit all data (assuming data represented as 32 bits real numbers) would take \(2,3 \times 10^{16}\ \mbox {s}\) or, equivalently, \(1.70 \times 10^{10}\) years (the estimated age of the universe is \(1.37 \times 10^{10}\) years).

If we wanted this to happen really fast, say in 1 millisecond, the transmission rate should be \(2.3 \times 10^{19}\) faster than the record they reached at CERN… something that is inconceivable for us today.