Duplicating Hankel plot from Abramowitz & Stegun

Nicolás Guarín-Zapata

2025-04-15 15:28

Also available in:

Recently, I had a discussion in class about solutions for partial differential equations and how visualization played a role way before digital computers were ubiquitous. We also discussed about the Handbook of Mathematical Functions or Abramowitz and Stegun [1] , as it is commonly called.

Luckily, John D. Cook replicated the following plot from Abramowitz and Stegun in his blog using Mathematica.

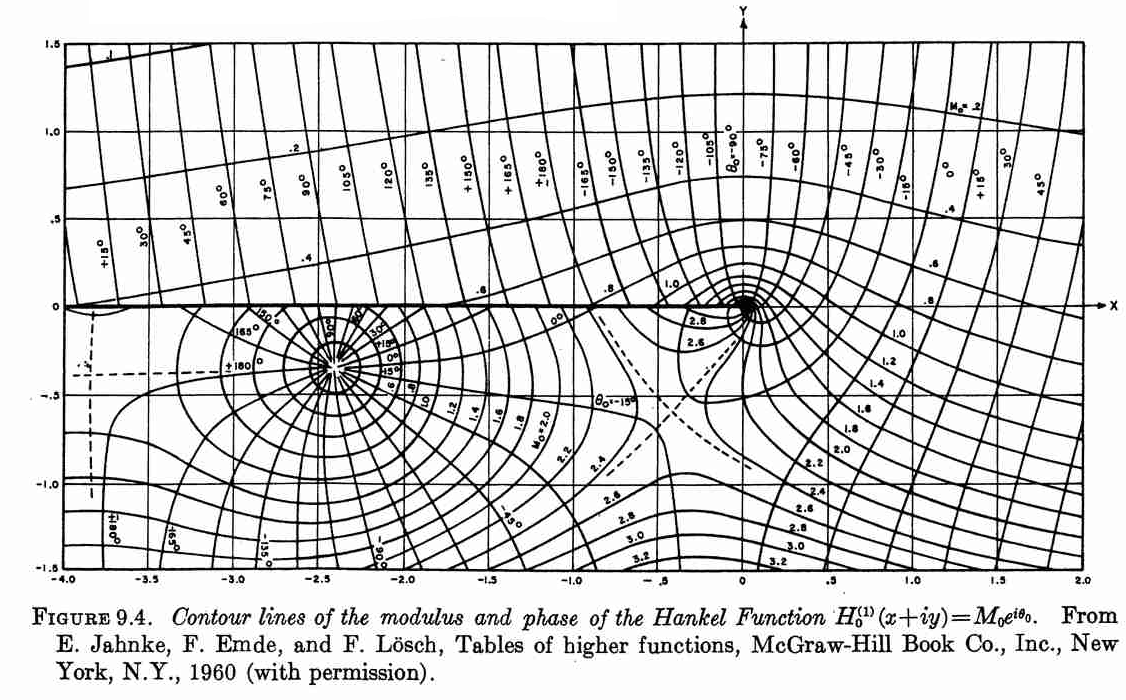
Contour plots for modulus and phase of the Hankel function over the complex plane.

So, I tried to replicate this figure using Matplotlib. The following plot is the result of using the contour function on the modulus and phase of the Hankel function.

This was obtained with the following code.

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import hankel1

y, x = np.mgrid[-1.5:1.5:2500j, -4:2:5000j]
z = x + 1j*y
H = hankel1(0, z)
abs_H = np.abs(H)
arg_H = np.rad2deg(np.angle(H))

fig, ax = plt.subplots(figsize=(12, 6))

plt.contour(x, y, abs_H, 20, colors="black")
plt.contour(x, y, arg_H, 30, colors="#757575")


plt.xticks(np.arange(-4, 2.5, 0.5))
plt.yticks(np.arange(-1.5, 2, 0.5))

plt.xlabel("Real axis")
plt.ylabel("Imaginary axis")

plt.grid("True")
plt.axis("image")
plt.savefig("abramowitz_stegun-hankel-0.svg", bbox_inches="tight")
plt.show()

There are some problems with the jump across the negative part of the real line. We can apply a mask with the following code:

abs_H[(x < 0) *  (np.abs(y) < 0.01)] = np.nan

Also, we have some problems around ±180° that correspond to the same phase value but the contour algorithm fails—maybe there is a variant of marching squares that allow to work with periodic data. To solve this issue I did the following, trick:

arg_H[arg_H < -179] += 360
arg_H[arg_H < -178] = np.nan

And we obtain the following figure.

We are missing the labels that show us the value of some of the contours. If we do it automatically, we obtain the following figure.

To obtain a figure closer to the original, Matplotlib has an optional parameter called manual that allows the user to place the labels of the contours manually.

The following figure is closer to the original.

The following snippet presents the code for the final version. You can download it here

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import hankel1


#%% Data
y, x = np.mgrid[-1.5:1.5:2500j, -4:2:5000j]
z = x + 1j*y
H = hankel1(0, z)

abs_H = np.abs(H)
abs_H[(x < 0) *  (np.abs(y) < 0.01)] = np.nan
levels_abs = np.arange(0.2, 3.3, 0.2)


arg_H = np.rad2deg(np.angle(H))
arg_H[(x < 0) *  (np.abs(y) < 0.01)] = np.nan
arg_H[arg_H < -179] += 360
arg_H[arg_H < -178] = np.nan
levels_arg = np.arange(-165, 181, 15)


#%% Plots setup
labels = True
manual_labels = True


#%% Ploting
fig, ax = plt.subplots(figsize=(12, 6))

# Jump line
plt.plot([-4, 0], [0, 0], color="black", linewidth=3, zorder=3)

# Contours
abs_contours = plt.contour(x, y, abs_H, levels_abs, colors="black",
                            linestyles="solid", zorder=4)
arg_contours = plt.contour(x, y, arg_H, levels_arg, colors="#757575",
                            linestyles="solid", zorder=6)

# Figure details
plt.xticks(np.arange(-4, 2.5, 0.5))
plt.yticks(np.arange(-1.5, 2, 0.5))

plt.xlabel("Real axis")
plt.ylabel("Imaginary axis")

plt.grid("True", color="#BDBDBD", zorder=3)
plt.axis("image")

# Labels
if labels:
    ax.clabel(abs_contours, levels_abs, fontsize=8, fmt="%.1f",
            use_clabeltext=True, manual=manual_labels, zorder=5)
    ax.clabel(arg_contours, levels_arg, fontsize=8, fmt="%d°",
            colors="#757575",
            use_clabeltext=True, manual=manual_labels, zorder=6)

plt.savefig("abramowitz_stegun-hankel-manual.svg", bbox_inches="tight")
plt.show()

Nicolás' blog

Comments